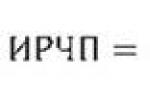Găsiți diferențialul funcției într-un punct dat. §24. Funcția diferențială. Semnificația geometrică a diferențialului unei funcții

De îndată ce nu am explicat (în acest moment) care este derivatul unei funcții, nu are sens să explic și care este diferențialul unei funcții. În cea mai primitivă formulare, un diferențial este „aproape la fel ca un derivat”.

Derivatul unei funcții este cel mai adesea notat cu.

Diferențialul unei funcții este notat în mod standard cu (și se citește - "de igrek")

Diferențialul unei funcții a unei variabile este scris după cum urmează:

O altă opțiune de înregistrare:

Sarcina cea mai simplă: Găsiți diferențialul unei funcții

1) Prima etapă. Găsiți derivatul:

2) A doua etapă. Să scriem diferențialul:

Diferențialul unei funcții a uneia sau mai multor variabile este cel mai des folosit pentru calcule aproximative.

Pe lângă alte sarcini cu diferențial, din când în când există o sarcină „pură” pentru a găsi diferențialul unei funcții. În plus, ca și pentru o derivată, pentru o diferențială există conceptul de diferențial într-un punct. Și vom lua în considerare și astfel de exemple.

Exemplul 7

Găsiți diferențialul unei funcții

Înainte de a găsi o derivată sau diferențială, este întotdeauna recomandabil să vedeți dacă este posibil să simplificați cumva funcția (sau să scrieți o funcție) inainte de diferenţiere? Să ne uităm la exemplul nostru. În primul rând, rădăcina poate fi transformată:

(a cincea rădăcină se referă în mod specific la sinus).

În al doilea rând, observăm că sub sinus avem o fracțiune, care evident trebuie diferențiată. Formula pentru diferențierea unei fracțiuni este foarte greoaie. Nu putem scăpa de fracțiune? În acest caz, putem, împărțim numărătorul la numitorul termen la termen:

Funcția este complexă. Are două atașamente: un sinus este imbricat sub grad, iar o expresie este imbricată sub sinus. Găsiți derivata folosind regula diferențierii unei funcții complexe de două ori:

Să notăm diferențialul, în timp ce îl prezentăm din nou în forma sa „frumoasă” originală:

Când derivatul este o fracțiune, pictograma este de obicei „lipicioasă” chiar la capătul numărătorului (este de asemenea posibil la dreapta la nivelul barei fracționare).

Exemplul 8

Găsiți diferențialul unei funcții

Acesta este un exemplu pentru o soluție de bricolaj.

Următoarele două exemple sunt pentru găsirea diferențialului într-un punct.

Exemplul 9

Calculați diferențialul unei funcții la punct

Găsiți derivatul:

Din nou, derivatul pare a fi găsit. Dar trebuie totuși să înlocuim un număr în acest bodyguard, așa că simplificăm rezultatul pe cât posibil:

Lucrarea nu a fost în zadar, scriem diferențialul:

Acum să calculăm diferențialul la punctul:

Nu trebuie să înlocuiți unitatea în insigna diferențială, este puțin dintr-o altă operă.

Dacă funcția diferențiat la punct , atunci creșterea sa poate fi reprezentată ca suma a doi termeni

... Acești termeni sunt funcții infinitesimale pentru
Primul termen este liniar în raport cu
, al doilea este infinit de mic de un ordin mai mare decât
.Într-adevăr,

.

Astfel, al doilea termen pentru
tinde la zero mai repede și la găsirea incrementului funcției
primul termen joacă rolul principal
sau (din moment ce
)
.

Definiție . Partea principală a funcției de incrementare
la punct , liniar în raport cu
,numit diferențial funcţie în acest moment și este notatdysaudf(X)

. (2)

Astfel, putem concluziona: diferențialul variabilei independente coincide cu creșterea acesteia, adică
.

Relația (2) ia acum forma

(3)

cometariu ... Pentru scurtitate, formula (3) este adesea scrisă ca

(4)

Semnificația geometrică a diferențialului

Luați în considerare graficul funcției diferențiabile
... Puncte
și aparțin funcției grafice. La punctul respectiv M tangent desenat LA la graficul funcției, unghiul căruia cu direcția pozitivă a axei
denotați prin
... Să desenăm drept MN paralel cu axa Bou și
paralel cu axa Oy... Incrementul funcției este egal cu lungimea segmentului
... Dintr-un triunghi dreptunghiular
, in care
, primim

Raționamentul de mai sus ne permite să concluzionăm:

Funcția diferențială
la punct este descris prin incrementarea ordonatei tangentei la graficul acestei funcții la punctul său corespunzător
.

Relația diferențială cu derivata

Luați în considerare formula (4)

.

Împărțim ambele părți ale acestei egalități cu dx, atunci

.

Prin urmare, derivata unei funcții este egală cu raportul diferențialului său cu diferențialul variabilei independente.

Adesea această atitudine este privit pur și simplu ca un simbol care denotă derivata unei funcții la prin argument NS.

Notarea derivată convenabilă este, de asemenea:

,
etc.

Se folosesc și înregistrări

,
,

convenabil mai ales atunci când se ia un derivat al unei expresii complexe.

2. Diferențial de sumă, produs și coeficient.

Deoarece diferențialul se obține din derivată prin multiplicarea acestuia cu diferențialul variabilei independente, atunci, cunoscând derivatele funcțiilor elementare de bază, precum și regulile pentru găsirea derivatelor, se poate ajunge la reguli similare pentru găsirea diferențialelor.

1 0 . Constanta diferențială este zero

.

2 0 . Diferențialul sumei algebrice a unui număr finit de funcții diferențiate este egal cu suma algebrică a diferențialelor acestor funcții

3 0 . Diferențialul produsului a două funcții diferențiate este egal cu suma produselor primei funcții prin diferențialul celei de-a doua și a doua funcții prin diferențialul primei funcții

.

Consecinţă. Un multiplicator constant poate fi scos din semnul diferențial

.

Exemplu... Găsiți diferențialul funcției.

Soluție: Să scriem această funcție ca

,

atunci ajungem

.

4. Funcții date parametric, diferențierea lor.

Definiție . Funcţie
se numește parametric dat dacă ambele variabile NS și la fiecare este definită separat ca funcții cu o singură valoare a aceleiași variabile auxiliare - parametrult:

Undetvariază în interior
.

cometariu ... Setarea parametrică a funcțiilor este utilizată pe scară largă în mecanica teoretică, unde parametrul t denotă timpul și ecuațiile
reprezintă legile schimbării în proiecțiile unui punct în mișcare
pe axă
și
.

cometariu ... Prezentăm ecuațiile parametrice ale unui cerc și ale unei elipse.

a) Un cerc cu un centru la origine și o rază r are ecuații parametrice:

Unde
.

b) Să scriem ecuațiile parametrice pentru elipsă:

Unde
.

Prin excluderea parametrului t din ecuațiile parametrice ale liniilor avute în vedere, se poate ajunge la ecuațiile lor canonice.

Teorema ... Dacă funcția y din argument x este dat parametric de ecuații
, Unde
și
diferențiat detfuncții și
, atunci

.

Exemplu... Găsiți derivata unei funcții la din NS date de ecuații parametrice.

Soluţie.
.

Fiind legați indisolubil, amândoi au fost folosiți activ timp de câteva secole pentru a rezolva aproape toate problemele apărute în procesul activității umane științifice și tehnice.

Apariția conceptului de diferențial

Faimosul matematician german Gottfried Wilhelm Leibniz, unul dintre fondatorii (împreună cu Isaac Newton) a calculului diferențial, a explicat mai întâi ce este un diferențial. Înainte de aceasta, matematicienii art. a folosit o idee foarte neclară și vagă a unei părți "indivizibile" infinit de mici a oricărei funcții cunoscute, reprezentând o valoare constantă foarte mică, dar care nu este egală cu zero, mai mică decât valorile funcției pur și simplu nu pot fi. De aici a existat un singur pas înainte de introducerea conceptului de creșteri infinit de mici ale argumentelor funcțiilor și ale creșterilor corespunzătoare ale funcțiilor în sine, exprimate în termenii derivatelor acestora din urmă. Și acest pas a fost făcut aproape simultan de cei doi mari oameni de știință menționați mai sus.

Pornind de la nevoia de a rezolva problemele practice urgente ale mecanicii, pe care industria și tehnologia în dezvoltare rapidă le-au pus înaintea științei, Newton și Leibniz au creat metode generale pentru a găsi rata de schimbare a funcțiilor (în primul rând în raport cu viteza mecanică de mișcare a unui corp de-a lungul unei traiectorii cunoscute), care a condus la introducerea unor astfel de concepte, ca derivată și diferențială a funcției, și a găsit, de asemenea, un algoritm pentru rezolvarea problemei inverse, cum să găsim calea parcursă de la o viteză cunoscută (variabilă), care a dus la apariția conceptului de integral.

În scrierile lui Leibniz și Newton, a apărut prima dată ideea că diferențialele sunt părțile principale ale incrementelor funcțiilor Δy proporționale cu incrementele argumentelor Δх, care pot fi aplicate cu succes pentru a calcula valorile acestora din urmă. Cu alte cuvinte, au descoperit că incrementarea unei funcții poate fi în orice punct (în domeniul definiției sale) exprimat în termenii derivatei sale ca Δу = y "(x) Δх + αΔх, unde α Δх este restul, tendința la zero ca Δх → 0 este mult mai rapidă decât Δx în sine.

Potrivit fondatorilor analizei matematice, diferențialele sunt exact primii termeni în expresii pentru incrementele oricărei funcții. Încă nu au un concept clar formulat al limitei secvențelor, au înțeles intuitiv că valoarea diferențialului tinde spre derivarea funcției ca Δх → 0 - Δу / Δх → y "(x).

Spre deosebire de Newton, care era în primul rând fizician, și considera aparatul matematic ca un instrument auxiliar pentru studiul problemelor fizice, Leibniz a acordat mai multă atenție acestui set de instrumente, inclusiv sistemului de denumiri vizuale și ușor de înțeles ale mărimilor matematice. El a propus notația general acceptată pentru diferențialele funcției dy = y "(x) dx, argumentul dx și derivatul funcției sub forma raportului lor y" (x) = dy / dx.

Definiție modernă

Ce este un diferențial din punctul de vedere al matematicii moderne? Este strâns legată de conceptul de increment variabil. Dacă variabila y ia mai întâi valoarea y = y 1, apoi y = y 2, atunci diferența y 2 ─ y 1 se numește creșterea lui y.

Creșterea poate fi pozitivă. negativ și egal cu zero. Cuvântul „increment” este notat cu Δ, înregistrarea Δy (citiți „joc delta”) denotă o creștere a valorii lui y. astfel încât Δу = y 2 ─ y 1.

Dacă valoarea Δу a unei funcții arbitrare y = f (x) poate fi reprezentată sub forma Δу = A Δх + α, unde A nu depinde de Δх, adică A = const pentru un х dat, iar termenul α tinde să este chiar mai rapid decât Δx în sine, atunci primul termen („principal”) proporțional cu Δx este pentru y = f (x) un diferențial notat cu dy sau df (x) (citiți „de igrek”, „de eff de la x "). Prin urmare, diferențialele sunt componentele „principale” ale incrementelor de funcții, liniare în raport cu Δх.

Interpretare mecanică

Fie s = f (t) distanța vehiculului care se deplasează în linie dreaptă față de poziția inițială (t este timpul petrecut pe drum). Incrementul Δs este calea punctului pe intervalul de timp Δt, iar diferențialul ds = f "(t) Δt este calea pe care ar fi parcurs-o punctul în același timp Δt dacă ar fi păstrat viteza f" (t ) atins până când ... Pentru un itest infinitesimal, calea imaginară ds diferă de trues adevărat printr-o valoare infinitesimală, care are un ordin mai mare față de Δt. Dacă viteza la timpul t nu este zero, atunci ds oferă o valoare aproximativă pentru mica deplasare a punctului.

Interpretarea geometrică

Fie dreapta L graficul lui y = f (x). Apoi Δ х = MQ, Δу = QM "(vezi figura de mai jos). Linia tangentă MN împarte segmentul Δу în două părți, QN și NM". Primul este proporțional cu Δх și este egal cu QN = MQ ∙ tg (unghiul QMN) = Δх f "(x), adică QN este dy-ul diferențial.

A doua parte NM "dă diferența Δу ─ dy, când Δх → 0 lungimea NM" scade chiar mai repede decât creșterea argumentului, adică are un ordin de micție mai mare decât cel al lui Δх. În cazul analizat, pentru f "(x) ≠ 0 (tangenta nu este paralelă cu OX), segmentele QM" și QN sunt echivalente; cu alte cuvinte, NM „scade mai repede (ordinea micuței sale este mai mare) decât creșterea totală Δу = QM”. Acest lucru poate fi văzut în figură (pe măsură ce M "se apropie de M, segmentul NM" reprezintă un procent mai mic din segmentul QM ").

Deci, grafic, diferențialul unei funcții arbitrare este egal cu creșterea ordonatei tangentei sale.

Derivată și diferențială

Coeficientul A din primul termen al expresiei pentru creșterea funcției este egal cu valoarea derivatei sale f "(x). Astfel, se ține următoarea relație - dy = f" (x) Δх sau df (x) = f "(x) Δх.

Se știe că creșterea unui argument independent este egală cu diferențialul său Δх = dx. În consecință, puteți scrie: f "(x) dx = dy.

Găsirea (uneori spusă, „rezolvarea”) diferențialelor se efectuează în conformitate cu aceleași reguli ca și pentru derivate. O listă a acestora este prezentată mai jos.

Ceea ce este mai universal: creșterea argumentului sau diferențialul său

Sunt necesare câteva clarificări aici. Reprezentarea diferențialului prin valoarea f "(x) Δх este posibilă atunci când x este considerat ca argument. Dar funcția poate fi complexă, în care x poate fi o funcție a unui argument t. Apoi reprezentarea diferențialului prin expresia f "(x) Δх este, de regulă, imposibilă; cu excepția cazului unei dependențe liniare x = at + b.

În ceea ce privește formula f "(x) dx = dy, atunci în cazul unui argument independent x (atunci dx = Δx), și în cazul unei dependențe parametrice a lui x de t, acesta reprezintă un diferențial.

De exemplu, expresia 2 x Δx reprezintă pentru y = x 2 diferențialul său când x este un argument. Acum punem x = t 2 și considerăm t ca argument. Atunci y = x 2 = t 4.

Această expresie nu este proporțională cu Δt și, prin urmare, acum 2xΔx nu este un diferențial. Se poate găsi din ecuația y = x 2 = t 4. Se dovedește a fi egal cu dy = 4t 3 Δt.

Dacă luăm expresia 2xdx, atunci reprezintă diferențialul y = x 2 pentru orice argument t. Într-adevăr, pentru х = t 2 obținem dx = 2tΔt.

Prin urmare, 2xdx = 2t 2 2tΔt = 4t 3 Δt, adică expresiile diferențialelor scrise în termeni de două variabile diferite au coincis.

Înlocuirea treptelor cu diferențiale

Dacă f "(x) ≠ 0, atunci Δу și dy sunt echivalente (când Δх → 0); când f" (x) = 0 (ceea ce înseamnă dy = 0), ele nu sunt echivalente.

De exemplu, dacă y = x 2, atunci Δy = (x + Δx) 2 ─ x 2 = 2xΔx + Δx 2 și dy = 2xΔx. Dacă x = 3, atunci avem Δу = 6Δх + Δх 2 și dy = 6Δх, care sunt echivalente datorită Δх 2 → 0, la x = 0 valorile Δу = Δх 2 și dy = 0 nu sunt echivalente.

Acest fapt, împreună cu structura simplă a diferențialului (adică liniaritatea față de Δx), este adesea utilizat în calcule aproximative, în ipoteza că Δу ≈ dy pentru Δх mic. Găsirea diferențialului unei funcții este de obicei mai ușoară decât calcularea valorii exacte a incrementului.

De exemplu, avem un cub metalic cu marginea x = 10,00 cm. Când este încălzit, marginea s-a lungit cu Δх = 0,001 cm. Cât a crescut volumul V al cubului? Avem V = x 2, deci dV = 3x 2 Δx = 3 ∙ 10 2 ∙ 0/01 = 3 (cm 3). Creșterea volumului ΔV este echivalentă cu diferențialul dV, astfel încât ΔV = 3 cm 3. Un calcul complet ar da ΔV = 10.01 3 ─ 10 3 = 3.003001. Dar în acest rezultat, toate numerele, cu excepția primului, nu sunt fiabile; ceea ce înseamnă, totuși, trebuie rotunjit până la 3 cm 3.

Evident, această abordare este utilă numai dacă este posibilă estimarea magnitudinii erorii introduse.

Funcția diferențială: exemple

Să încercăm să găsim diferențialul funcției y = x 3 fără a găsi derivata. Să dăm argumentului o creștere și să definim Δу.

Δу = (Δх + x) 3 ─ x 3 = 3x 2 Δх + (3xΔх 2 + Δх 3).

Aici coeficientul A = 3x 2 nu depinde de Δx, astfel încât primul termen este proporțional cu Δx, în timp ce celălalt termen 3xΔx 2 + Δx 3 scade mai repede decât creșterea argumentului ca Δx → 0. Prin urmare, termenul 3x 2 Δx este diferențialul y = x 3:

dy = 3x 2 Δx = 3x 2 dx sau d (x 3) = 3x 2 dx.

Mai mult, d (x 3) / dx = 3x 2.

Să găsim acum dy al funcției y = 1 / x din punct de vedere al derivatei sale. Apoi d (1 / x) / dx = ─1 / x 2. Prin urmare, dy = ─ Δх / х 2.

Diferențialele funcțiilor algebrice de bază sunt date mai jos.

Aproximare diferențială

Este adesea ușor să calculați funcția f (x), precum și derivata sa f "(x) pentru x = a, dar nu este ușor să faceți același lucru în vecinătatea punctului x = a. Apoi o aproximare expresia vine în ajutor

f (a + Δх) ≈ f "(a) Δх + f (a).

Oferă o valoare aproximativă a funcției la mici trepte Δх prin diferențialul său f "(a) Δх.

Prin urmare, această formulă oferă o expresie aproximativă pentru funcția la punctul final al unei anumite secțiuni de lungime Δx ca suma valorii sale la punctul de plecare al acestei secțiuni (x = a) și diferențialul la același punct de plecare. Eroarea acestei metode de determinare a valorii unei funcții este ilustrată în figura de mai jos.

Cu toate acestea, expresia exactă pentru valoarea funcției pentru x = a + Δх este, de asemenea, cunoscută, dată de formula incrementelor finite (sau, în caz contrar, de formula Lagrange)

f (a + Δх) ≈ f "(ξ) Δх + f (a),

unde punctul x = a + ξ este situat pe intervalul de la x = a la x = a + Δх, deși poziția sa exactă este necunoscută. Formula exactă vă permite să estimați eroarea formulei aproximative. Dacă punem ξ = Δx / 2 în formula Lagrange, atunci deși încetează să fie exactă, de obicei oferă o aproximare mult mai bună decât expresia originală în ceea ce privește diferențialul.

Estimarea erorii formulelor folosind diferențialul

În principiu, acestea sunt inexacte și introduc erori corespunzătoare în datele de măsurare. Acestea se caracterizează prin eroarea limitativă sau, pe scurt, eroarea limitativă - un număr pozitiv, care depășește în mod evident această eroare în valoare absolută (sau, în cazuri extreme, egală cu aceasta). Limita se numește coeficientul diviziunii sale la valoarea absolută a valorii măsurate.

Să se utilizeze formula exactă y = f (x) pentru a calcula funcția y, dar valoarea x este rezultatul măsurării și, prin urmare, introduce o eroare în y. Apoi, pentru a găsi eroarea absolută limitativă │‌‌Δу│ a funcției y, utilizați formula

│‌‌Δу│≈│‌‌dy│ = │ f "(x) ││Δх│,

unde │Δх│ este eroarea limitativă a argumentului. Valoarea │‌‌Δу│ ar trebui rotunjită în sus, deoarece este inexact să înlocuiască calculul incrementului cu calculul diferențialului.

CONFERINȚĂ 10. FUNCȚII DIFERENȚIALE. TEOREMA FERMEI, ROLULUI, LAGRANGE ȘI CAUCHIE.

1. Funcția diferențială

1.1. Determinarea diferențialului unei funcții

CU conceptul derivatului este strâns legat de un alt concept fundamental de analiză matematică - diferențialul unei funcții.

Definiție 1. O funcție y = f (x) definită într-o vecinătate a unui punct x se numește diferențiată la un punct x dacă creșterea sa în acest punct

y = f (x + x) - f (x)

are forma

y = A x + α (Δx) x,

unde A este o constantă și funcția α (Δx) → 0 ca x → 0.

Fie y = f (x) o funcție diferențiată, atunci dăm următoarea definiție.

Definiție 2. Liniar principal		partea A x	trepte	funcția f (x)
se numește diferențialul funcției la punctul x și se notează cu dy.
Prin urmare,
y = dy + α (Δx) x.
Observație 1. Cantitatea dy =		x se numește	partea liniară principală
incrementul y datorită faptului că cealaltă parte a incrementului α (Δx)				x pentru mici
x devine mult mai mic decât A

Enunț 1. Pentru ca funcția y = f (x) să fie diferențiată la punctul x, este necesar și suficient ca aceasta să aibă o derivată în acest moment.

Dovadă. Nevoie. Funcția f (x) să fie diferențiată în acest punct

x + α (Δx) x, pentru

x → 0. Apoi

A + lim α (Δx) = A.

Prin urmare, derivata f ′ (x) există și este egală cu A.

Adecvare. Să existe

f ′ (x), adică există o limită limită

F ′ (x).

F ′ (x) + α (Δx),

y = f ′ (x) Δx + α (Δx) x.

Ultima egalitate înseamnă diferențialitatea funcției y = f (x).

1.2. Semnificația geometrică a diferențialului

Fie l tangenta graficului funcției y = f (x) în punctul M (x, f (x)) (Fig. 1). Să arătăm că dy este valoarea segmentului P Q. Într-adevăr,

dy = f ′ (x) Δx = tan α x =

"" l

"" " "

" α

Deci, diferențialul dy al funcției f (x) în punctul x este egal cu creșterea ordonatei tangentei l în acest punct.

1.3. Formați invarianța diferențialului

Dacă x este o variabilă independentă, atunci

dy = f ′ (x) dx.

Să presupunem că x = ϕ (t), unde t este o variabilă independentă, y = f (ϕ (t)). Atunci

dy = (f (ϕ (t)) ′ dt = f ′ (x) ϕ ′ (t) dt = f ′ (x) dx (ϕ ′ (t) dt = dx).

Deci, forma diferențialului nu s-a schimbat, în ciuda faptului că x nu este o variabilă independentă. Această proprietate se numește invarianța formei diferențialului.

1.4. Aplicare diferențială în calcule aproximative

Din formula y = dy + α (Δx) x, aruncând α (Δx) x, se vede că pentru mici

y ≈ dy = f ′ (x) Δx.

De aici ajungem

f (x + x) - f (x) ≈ f ′ (x) Δx,

f (x + x) ≈ f (x) + f ′ (x) Δx. (1) Formula (1) și este utilizată în calcule aproximative.

1.5. Diferențiale de ordin superior

Prin definiție, al doilea diferențial al funcției y = f (x) la un punct x se numește diferențial al primului diferențial în acest punct, care este notat

d2 y = d (dy).

Să calculăm al doilea diferențial:

d2 y = d (dy) = d (f ′ (x) dx) = (f ′ (x) dx) ′ dx = (f ′ ′ (x) dx) dx = f ′ ′ (x) dx2

(la calcularea derivatei (f ′ (x) dx) ′ s-a avut în vedere faptul că cantitatea dx nu depinde de x și, prin urmare, este constantă în timpul diferențierii).

În general, diferențialul de ordine n al unei funcții y = f (x) este primul

diferenţial

din diferențial

această funcție care

notat cu

dn y = d (dn - 1 y)

dn y = f (n) (x) dxn.

Găsiți diferențialul funcției y = arctan x.

Soluţie. dy = (arctan x) ′ dx =

1 + x2

Găsiți diferențialele primelor și celui de-al doilea ordine ale funcției v = e2t.

Soluţie. dv = 2e2t dt, d2 v = 4e2t dt2.

Comparați incrementul și diferențialul funcției y = 2x3 + 5x2.

Soluţie. Găsim

5x2 =

10x) Δx + (6x + 5) Δx

dy = (6x2 + 10x) dx.

Diferența dintre increment

y și dy diferențial este infinitesimalul mai mare

ordin comparativ cu

x egal cu (6x + 5) Δx2 + 2Δx3.

Exemplul 4. Calculați valoarea aproximativă a ariei unui cerc, a cărui rază este de 3,02 m.

Soluţie. Să folosim formula S = πr2. Setarea r = 3, r = 0,02, avem

S ≈ dS = 2πr r = 2π 3 0,02 = 0,12π.

Prin urmare, valoarea aproximativă a ariei unui cerc este 9π + 0, 12π = 9, 12π ≈

28, 66 (m 2).

Exemplul 5. Calculați valoarea aproximativă a arcurilor în 0, 51 cu o precizie de 0,001. Soluţie. Luați în considerare funcția y = arcsin x. Setarea x = 0,5, x = 0,01 și

aplicarea formulei (1)

x) ≈ arcsin x + (arcsin x) ′

(arcsin x) ′

≈ arcsin 0,5 +

0, 011 = 0, 513.

1 − (0, 5)2

Exemplul 6. Calculați aproximativ √ 3

precis la 0.0001.

Soluţie. Luați în considerare funcția y = √ 3

și pune x = 8,

x = 0, 01. În mod similar

conform formulei (1)

(√ 3 x) ′ =

√3

√ x + x ≈ √ 3 x + (√ 3 x) ′ x,

3√ 3 64

0,01 = 2 + 3.40.01 ≈ 2.0008.

p 8.01 ≈ √ 8 +

2. Teoremele lui Fermat, Rolle, Lagrange și Cauchy

Definiție 3. Se spune că funcția y = f (x) are (sau atinge) un maxim local (minim) în punctul α dacă există o vecinătate U (α) a punctului α astfel încât pentru toate x U (α ):

f (α) ≥ f (x) (f (α) ≤ f (x)).

Maxim local și minim local sunt unite printr-un nume comun

extremum local.

Funcția, al cărei grafic este prezentat în Fig. 4, are un maxim local în punctele β, β1 și un minim local în punctele α, α1.

Enunțul 2. (Fermat) Fie funcția y = f (x) diferențiată în punctul α și să aibă un extrem local în acest punct. Atunci f ′ (α) = 0.

Ideea din spatele dovezii teoremei lui Fermat este următoarea. Fie, pentru claritate, f (x) să aibă un minim local în punctul α. Prin definiție, f ′ (α) este limita ca x → 0 a raportului

	f (α + x) - f (α)
Dar pentru suficient de mic (în valoare absolută) x
	f (α + x) - f (α) ≥ 0.
Prin urmare, pentru asemenea	x primim
De aici rezultă că
	f ′ (α) = lim g (Δx) = 0.
Faceți singur dovada completă.
Declarația 3. (Roll)	Dacă y = f (x) este continuu pornit			Diferențiat de
(a, b) și f (a) = f (b), atunci există un punct α (a, b),				că f ′ (α) = 0.

Dovadă. Prin proprietatea funcțiilor care sunt continue pe un interval, există puncte x1, x2 astfel încât

extremum. Prin ipoteza teoremei, f (x) este diferențiat în punctul α. Prin teorema lui Fermat f ′ (α) = 0. Teorema este demonstrată.

Teorema lui Rolle are o semnificație geometrică simplă (Fig. 5): dacă ordinele extreme ale curbei y = f (x) sunt egale, atunci pe curba y = f (x) există un punct în care tangenta curbei este paralel cu axa Ox.

Enunțul 4. (Cauchy) Fie f (x), g (x) să fie continuu pe, diferențiat pe (a, b) și g ′ (x) = 6 0 pentru orice x (a, b). Apoi există un punct α (a, b) astfel încât

		f ′ (α)
		g ′ (α)

Dovadă. Rețineți că g (a) = 6 g (b). Într-adevăr, altfel funcția g (x) ar satisface toate condițiile teoremei lui Rolle. În consecință, ar exista un punct β (a, b) astfel încât g ′ (β) = 0. Dar acest lucru contrazice ipoteza teoremei.

Luați în considerare următoarea funcție de ajutor:

F (x) = f (x) - f (a) - f (b) - f (a) (g (x) - g (a)). g (b) - g (a)

Funcția F (x) este continuă activată,				diferențiat pe (a, b). Mai mult, este evident că
ce'	F (a) = F (b) = 0. Prin urmare, conform teoremei lui Rolle, există un punct α (a, b) astfel încât
F (α) = 0, adică
	f ′ (α)								g ′ (α) = 0.
			- g (b)
asta implică
								f ′ (α)
								g ′ (α)

Teorema este dovedită.

Enunțul 5. (Lagrange) Dacă y = f (x) este continuu pe, diferențiat pe (a, b), atunci există α (a, b) astfel încât

F ′ (α).

Dovadă. Teorema lui Lagrange urmează direct din teorema lui Cauchy pentru g (x) =

Geometric, teorema lui Lagrange înseamnă că pe curba y = f (x) dintre puncte

A și B, există un punct C în care tangenta este paralelă cu coarda AB. y

Soluţie. Deoarece funcția f (x) este continuă și diferențiată pentru toți

valorile lui x și valorile acestuia la capetele segmentului				Egal: f (1) = f (5)
Teorema lui Rolle pe acest segment		efectuat. Valoarea C					defini		ecuații
f ′ (x) = 2x - 6 = 0, adică c = 3.						gaseste un punct		M în care
Exemplul 8. Pe un arc		Curba AB y = 2x - x
tangentă paralelă cu coarda
Soluţie. Funcția y = 2x −x			continuă și diferențiată pentru toate valorile
X. Prin teorema lui Lagrange, între două valori a = 1,							b = 3 există valoarea

x = c satisfacerea egalității y (b) - y (a) = (b - a) y ′ (c), unde y ′ = 2 - 2x. Înlocuind valorile corespunzătoare, obținem

y (3) - y (1) = (3 - 1) y ′ (c),

(2 3 - 32) - (2 1 - 12) = (3 - 1) (2 - 2s),

deci c = 2, y (2) = 0.

Astfel, punctul M are coordonate (2; 0).

Exemplul 9. Pe arcul AB al curbei dat de ecuații parametrice

x = t2, y = t3, găsiți punctul

M în care linia tangentă este paralelă cu coarda AB dacă

punctele A și B corespund valorilor t = 1 și t = 3.

Soluţie. Panta coardei AB este

Și panta este

tangenta la punctul M (pt

t = c) este egal cu

y ′

(c) / x ′

x ′ = 2t,

y ′ = 3t2. Pentru

definind c prin teorema lui Cauchy, obținem ecuația

yt ′ (c)

xt ′ (c)

adică c = 13/6.

Valoarea găsită a lui c satisface inegalitatea 1< c < 3. Подставив значение t = c в параметрические уравнения кривой, получаем x = 169/36, y = 2197/216. Итак искомая точка M (169/36; 2197/216).