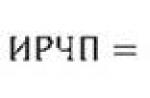Ce numere sunt iraționale? Număr irațional Nu este un număr real rațional, adică nu poate fi reprezentat ca o fracție (ca raportul a două numere întregi), unde m- un număr întreg, n- numar natural . Număr irațional poate fi gândit ca o fracție zecimală neperiodică infinită.
Număr irațional nu poate fi precis. Numai în formatul 3.333333…. De exemplu, rădăcina pătrată a două este un număr irațional.
Ce număr este irațional? Număr irațional(spre deosebire de rațional) se numește o fracție zecimală neperiodică infinită.
O mulțime de numere iraționale des denotată de o literă latină cu majuscule cu caractere aldine, fără completare. Acea.:
Acestea. mulțimea numerelor iraționale este diferența dintre mulțimile numerelor reale și raționale.
Proprietățile numerelor iraționale.
- Suma a 2 numere iraționale non-negative poate fi un număr rațional.
- Numerele iraționale definesc secțiunile Dedekind în setul numerelor raționale, în clasa inferioară care nu au cel mai mare număr, iar în clasa superioară nu există una mai mică.
- Orice număr transcendental real este un număr irațional.
- Toate numerele iraționale sunt fie algebrice, fie transcendentale.
- Setul de numere iraționale este peste tot dens pe linia numerică: între fiecare pereche de numere există un număr irațional.
- Ordinea pe mulțimea numerelor iraționale este izomorfă pentru ordinea pe mulțimea numerelor reale transcendentale.
- Mulțimea numerelor iraționale este infinită, este un set din a doua categorie.
- Rezultatul fiecărei operații aritmetice cu numere raționale (cu excepția împărțirii cu 0) este un număr rațional. Rezultatul operațiilor aritmetice pe numere iraționale poate fi atât un număr rațional, cât și un număr irațional.
- Suma unui număr rațional și a unui număr irațional va fi întotdeauna un număr irațional.
- Suma numerelor iraționale poate fi un număr rațional. De exemplu, lasa X irațional atunci y = x * (- 1) de asemenea irațional; x + y = 0,și numărul 0 rațional (dacă, de exemplu, adăugând o rădăcină de orice grad de 7 și minus o rădăcină de același grad de șapte, atunci obținem un număr rațional 0).
Numere iraționale, exemple.
γ — ζ (3) — ρ — √2 — √3 — √5 — φ — δs — α — e — π — δ
Vechii matematicieni știau deja cu un segment de lungime a unității: știau, de exemplu, incomensurabilitatea diagonalei și a laturii unui pătrat, ceea ce echivalează cu iraționalitatea unui număr.
Iraționale sunt:
Exemple de dovezi ale iraționalității
Rădăcina a 2
Să presupunem opusul: rațional, adică reprezentat ca o fracție ireductibilă, unde și sunt numere întregi. Să pătrăm egalitatea presupusă:
.De aici rezultă că înseamnă chiar și și. Să fie, unde este întregul. Atunci
Prin urmare, chiar înseamnă chiar și. Am obținut acest lucru și suntem uniformi, ceea ce contrazice ireductibilitatea fracției. Aceasta înseamnă că presupunerea inițială a fost greșită și - un număr irațional.
Logaritm binar de 3
Să presupunem opusul: rațional, adică reprezentat ca o fracție, unde și sunt numere întregi. Deoarece, și poate fi ales pozitiv. Atunci
Dar pare și ciudat. Avem o contradicție.
e
Istorie
Conceptul numerelor iraționale a fost adoptat implicit de matematicienii indieni în secolul al VII-lea î.Hr., când Manava (c. 750 î.Hr. - c. 690 î.Hr.) a constatat că rădăcinile pătrate ale unor numere naturale, precum 2 și 61 nu pot fi exprimate în mod explicit .
Prima dovadă a existenței numerelor iraționale este de obicei atribuită lui Hippasus din Metapont (c. 500 î.Hr.), un pitagoric care a găsit această dovadă studiind lungimile laterale ale pentagramei. În vremea pitagoreicilor, se credea că există o singură unitate de lungime, suficient de mică și indivizibilă, care intră în orice segment de un număr întreg de ori. Cu toate acestea, Hippasus a demonstrat că nu există o singură unitate de lungime, deoarece presupunerea existenței sale duce la o contradicție. El a arătat că, dacă ipotenuza unui triunghi unghiular isoscel conține un număr întreg de segmente unitare, atunci acest număr trebuie să fie atât par, cât și impar în același timp. Dovada arăta astfel:
- Raportul dintre lungimea hipotenuzei și lungimea piciorului unui triunghi dreptunghic isoscel poate fi exprimat ca A:b, Unde Ași b selectat ca fiind cel mai mic posibil.
- Prin teorema lui Pitagora: A² = 2 b².
- pentru că A² chiar, A trebuie să fie par (deoarece pătratul unui număr impar ar fi impar).
- În măsura în care A:b ireductibil b trebuie să fie ciudat.
- pentru că A chiar, denotați A = 2y.
- Atunci A² = 4 y² = 2 b².
- b² = 2 y², deci b Este uniform, atunci b chiar.
- Cu toate acestea, s-a dovedit că b ciudat. Contradicţie.
Matematicienii greci au numit acest raport de cantități incomensurabile aalogos(nespus), însă, conform legendelor, nu i-au acordat lui Hippas respectul pe care îl merita. Legenda spune că Hippasus a făcut o descoperire în timpul unei călătorii pe mare și a fost aruncat peste bord de alți pitagorici „pentru crearea unui element al universului care neagă doctrina că toate entitățile din univers pot fi reduse la numere întregi și la relațiile lor”. Descoperirea lui Hippasus a pus o problemă serioasă pentru matematica pitagorică, distrugând ipoteza care stă la baza întregii teorii conform căreia numerele și obiectele geometrice sunt una și inseparabilă.
Vezi si
Note (editați)
| Sisteme numerice | |
|---|---|
| Socoteală mulțimi |
Numere întregi () |
Am arătat deja că $ 1 \ frac25 $ este aproape de $ \ sqrt2 $. Dacă ar fi exact $ \ sqrt2 $ ,. Apoi, raportul - $ \ frac (1 \ frac25) (1) $, care poate fi transformat în raportul numerelor întregi $ \ frac75 $, înmulțind părțile superioare și inferioare ale fracției cu 5 și ar fi valoarea dorită.
Din păcate, $ 1 \ frac25 $ nu este o valoare exactă pentru $ \ sqrt2 $. Un răspuns mai precis $ 1 \ frac (41) (100) $, ne oferă relația $ \ frac (141) (100) $. Obținem o precizie și mai mare atunci când echivalăm $ \ sqrt2 $ cu $ 1 \ frac (207) (500) $. În acest caz, raportul în numere întregi va fi $ \ frac (707) (500) $. Dar, de asemenea, $ 1 \ frac (207) (500) $ nu este valoarea exactă a rădăcinii pătrate din 2. Matematicienii greci au petrecut mult timp și eforturi pentru a calcula valoarea exactă a $ \ sqrt2 $, dar nu au reușit niciodată. Nu au putut reprezenta raportul $ \ frac (\ sqrt2) (1) $ ca raport de numere întregi.
În cele din urmă, marele matematician grec Euclid a demonstrat că, indiferent de cât crește acuratețea calculelor, este imposibil să se obțină valoarea exactă de $ \ sqrt2 $. Nu există nicio fracțiune care, la pătrat, să ducă la 2. Se spune că Pitagora a fost primul care a ajuns la această concluzie, dar acest fapt inexplicabil a uimit atât de mult omul de știință, încât el însuși a jurat și a depus jurământul studenților săi pentru a păstra această descoperire. un secret ... Cu toate acestea, este posibil ca aceste informații să nu corespundă realității.
Dar dacă numărul $ \ frac (\ sqrt2) (1) $ nu poate fi reprezentat ca un raport de numere întregi, atunci niciunul nu conține $ \ sqrt2 $, de exemplu $ \ frac (\ sqrt2) (2) $ sau $ \ frac ( 4) (\ sqrt2) $, de asemenea, $ nu poate fi reprezentat ca un raport de numere întregi, deoarece toate aceste fracții pot fi convertite în $ \ frac (\ sqrt2) (1) $ înmulțit cu un anumit număr. Deci $ \ frac (\ sqrt2) (2) = \ frac (\ sqrt2) (1) \ times \ frac12 $. Sau $ \ frac (\ sqrt2) (1) \ times 2 = 2 \ frac (\ sqrt2) (1) $, care poate fi transformat înmulțind partea de sus și de jos cu $ \ sqrt2 $ pentru a obține $ \ frac (4) (\ sqrt2) $. (Amintiți-vă că indiferent care este numărul $ \ sqrt2 $, dacă îl înmulțim cu $ \ sqrt2 $, obținem 2.)
Deoarece numărul $ \ sqrt2 $ nu poate fi reprezentat ca un raport de numere întregi, se numește număr irațional... Pe de altă parte, se numesc toate numerele care pot fi reprezentate ca raport de numere întregi raţional.
Toate numerele întregi și fracționate, atât pozitive cât și negative, sunt raționale.
După cum se dovedește, majoritatea rădăcinilor pătrate sunt numere iraționale. Numai numerele dintr-o serie de numere pătrate au rădăcini pătrate raționale. Aceste numere se mai numesc pătrate perfecte. Numerele raționale sunt, de asemenea, fracții formate din aceste pătrate perfecte. De exemplu, $ \ sqrt (1 \ frac79) $ este un număr rațional deoarece $ \ sqrt (1 \ frac79) = \ frac (\ sqrt16) (\ sqrt9) = \ frac43 $ sau $ 1 \ frac13 $ (4 este rădăcină pătrată de 16, iar 3 este rădăcina pătrată a lui 9).
Materialul din acest articol oferă informații inițiale despre numere irationale... În primul rând, vom da o definiție a numerelor iraționale și o vom explica. Mai jos sunt exemple de numere iraționale. În cele din urmă, să analizăm câteva abordări pentru a afla dacă un anumit număr este sau nu irațional.
Navigare în pagină.
Definiție și exemple de numere iraționale
Când studiem fracții zecimale, am considerat separat fracții zecimale neperiodice infinite. Astfel de fracții apar atunci când lungimile zecimale ale segmentelor sunt măsurate necorespunzător cu un segment de unitate. Am observat, de asemenea, că fracțiile zecimale neperiodice infinite nu pot fi convertite în fracții (a se vedea conversia fracțiilor ordinare în zecimale și invers), prin urmare, aceste numere nu sunt numere raționale, ele reprezintă așa-numitele numere iraționale.
Așa că am ajuns la definirea numerelor iraționale.
Definiție.
Se numesc numere care reprezintă fracții zecimale neperiodice infinite în notație zecimală numere irationale.
Definiția sunată vă permite să aduceți exemple de numere iraționale... De exemplu, fracția zecimală neperiodică infinită 4.10110011100011110000 ... (numărul de unități și zerouri crește cu unul de fiecare dată) este un număr irațional. Să dăm un alt exemplu de număr irațional: −22.353335333335 ... (numărul de triple care separă optul este mărit cu două de fiecare dată).
Trebuie remarcat faptul că numerele iraționale sunt rareori găsite cu precizie sub forma unor fracții zecimale neperiodice infinite. De obicei, acestea se găsesc sub formă etc., precum și sub formă de litere introduse special. Cele mai faimoase exemple de numere iraționale din această notație sunt rădăcina pătrată aritmetică a doi, pi = 3,141592 ..., e = 2,718281 ... și numărul de aur.
Numerele iraționale pot fi definite și în termeni de numere reale, care combină numere raționale și iraționale.
Definiție.
Numere irationale Sunt numere reale care nu sunt raționale.
Este acest număr irațional?
Când un număr este dat nu sub forma unei fracții zecimale, ci sub forma unor, rădăcină, logaritm etc., atunci este destul de dificil să răspundem la întrebarea dacă este irațional în multe cazuri.
Fără îndoială, atunci când răspundeți la această întrebare, este foarte util să știți care numere nu sunt iraționale. Din definiția numerelor iraționale rezultă că numerele raționale nu sunt numere iraționale. Astfel, numerele iraționale NU sunt:
- zecimale periodice finite și infinite.
De asemenea, orice compoziție a numerelor raționale legate de semne ale operațiilor aritmetice (+, -, ·, :) nu este un număr irațional. Acest lucru se datorează faptului că suma, diferența, produsul și coeficientul a două numere raționale este un număr rațional. De exemplu, valorile expresiilor și sunt numere raționale. Aici observăm că dacă în astfel de expresii dintre numerele raționale există un singur număr irațional, atunci valoarea întregii expresii va fi un număr irațional. De exemplu, în expresie, numărul este irațional, iar restul numerelor sunt raționale, prin urmare, un număr irațional. Dacă ar fi un număr rațional, atunci raționalitatea numărului ar urma din aceasta, dar nu este rațională.
Dacă expresia pentru care este dat numărul conține mai multe numere iraționale, semne rădăcină, logaritmi, funcții trigonometrice, numere π, e etc., atunci este necesar să se demonstreze iraționalitatea sau raționalitatea numărului dat în fiecare caz specific. Cu toate acestea, există o serie de rezultate deja obținute care pot fi utilizate. Să enumerăm principalele.
Se dovedește că o rădăcină de grad k dintr-un număr întreg este un număr rațional numai dacă numărul de sub rădăcină este a k-a putere a unui alt număr întreg; în alte cazuri, o astfel de rădăcină definește un număr irațional. De exemplu, numerele și sunt iraționale, deoarece nu există un număr întreg al cărui pătrat este 7 și nu există un număr întreg a cărui creștere la a cincea putere să dea numărul 15. Și numerele și nu sunt iraționale, precum și.
În ceea ce privește logaritmii, este uneori posibil să se demonstreze iraționalitatea lor prin contradicție. De exemplu, să dovedim că log 2 3 este un număr irațional.
Să presupunem că log 2 3 este un număr rațional, nu irațional, adică poate fi reprezentat ca o fracție obișnuită m / n. și vă permit să scrieți următorul lanț de egalități :. Ultima egalitate este imposibilă, deoarece pe partea stângă numar impar, iar în dreapta - chiar. Așa că am ajuns la o contradicție, ceea ce înseamnă că presupunerea noastră sa dovedit a fi incorectă, iar acest lucru a dovedit că log 2 3 este un număr irațional.
Rețineți că lna este un număr irațional pentru orice rațional care este pozitiv și diferit de unitate. De exemplu, și sunt numere iraționale.
S-a dovedit, de asemenea, că numărul e a pentru orice rațional a zero este irațional și că numărul π z pentru orice număr întreg nenul z este irațional. De exemplu, numerele sunt iraționale.
Numerele iraționale sunt, de asemenea, funcții trigonometrice sin, cos, tg și ctg pentru orice valoare rațională și nenulă a argumentului. De exemplu sin1, tg (−4), cos5,7 sunt numere iraționale.
Există și alte rezultate dovedite, dar ne vom limita la cele deja enumerate. De asemenea, ar trebui spus că în dovada rezultatelor sunate mai sus, teoria asociată cu numere algebriceși numere transcendentale.
În concluzie, observăm că nu ar trebui să se facă concluzii pripite cu privire la iraționalitatea numerelor date. De exemplu, pare clar că un număr irațional într-un grad irațional este un număr irațional. Cu toate acestea, acest lucru nu este întotdeauna cazul. Ca o confirmare a faptului exprimat, acordăm gradul. Se știe că este un număr irațional și se dovedește, de asemenea, că este un număr irațional, dar este un număr rațional. De asemenea, puteți da exemple de numere iraționale, a căror sumă, diferență, produs și coeficient sunt numere raționale. Mai mult, raționalitatea sau iraționalitatea numerelor π + e, π - e, π · e, π π, π e și multe altele nu au fost încă dovedite.
Bibliografie.
- Matematica. Nota 6: manual. pentru învățământul general. instituții / [N. Da. Vilenkin și alții]. - ediția a 22-a, Rev. - M.: Mnemosina, 2008 .-- 288 p.: Bolnav. ISBN 978-5-346-00897-2.
- Algebră: studiu. pentru 8 cl. educatie generala. instituții / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; ed. S. A. Telyakovsky. - ediția a XVI-a - M .: Educație, 2008. - 271 p. : bolnav. - ISBN 978-5-09-019243-9.
- Gusev V.A., Mordkovich A.G. Matematică (manual pentru solicitanții școlilor tehnice): manual. manual. - M.; Superior. shk., 1984.-351 p., bolnav.
Din abstractitatea conceptelor matematice emană uneori atât de mult distanță, încât gândul apare involuntar: „De ce este totul?”. Dar, în ciuda primei impresii, toate teoremele, operațiile aritmetice, funcțiile etc. - nimic mai mult decât dorința de a satisface nevoile urgente. Acest lucru poate fi văzut în mod clar în exemplul apariției diferitelor seturi.
Totul a început cu apariția numerelor naturale. Și, deși este puțin probabil ca acum cineva să poată răspunde exact cum a fost, dar cel mai probabil, picioarele reginei științelor cresc de undeva din peșteră. Aici, analizând numărul de piei, pietre și oameni ai tribului, o persoană este o multitudine de „numere de numărat”. Și asta i-a fost suficient. Până la un anumit moment, desigur.
Apoi a fost necesar să împărțiți și să luați piei și pietre. Așadar, a apărut necesitatea operațiilor aritmetice și, împreună cu ele, raționale, care pot fi definite ca o fracțiune de tipul m / n, unde, de exemplu, m este numărul de piei, n este numărul de oameni ai tribului.
S-ar părea că aparatul matematic deja deschis este suficient pentru a vă bucura de viață. Dar s-a dovedit curând că cazurile în care rezultatul nu este ceva care nu este un număr întreg, dar nici măcar o fracțiune! Într-adevăr, rădăcina pătrată a doi nu poate fi exprimată în alt mod folosind numeratorul și numitorul. Sau, de exemplu, binecunoscutul număr Pi, descoperit de vechiul savant grec Arhimede, nu este nici el rațional. Și în timp, astfel de descoperiri au devenit atât de numeroase încât toate numerele care nu s-au împrumutat „raționalizării” au fost combinate și numite iraționale.
Proprietăți
Seturile luate în considerare anterior aparțin setului de concepte fundamentale ale matematicii. Aceasta înseamnă că nu pot fi definite în termeni de obiecte matematice mai simple. Dar acest lucru se poate face cu ajutorul categoriilor (din „afirmațiile” grecești) sau ale postulatelor. În acest caz, cel mai bine a fost să desemnați proprietățile acestor seturi.
o Numerele iraționale definesc secțiunile Dedekind în setul numerelor raționale, care nu au cel mai mare număr în cel inferior și cel mai mic număr în cel superior.
o Fiecare număr transcendental este irațional.
o Fiecare număr irațional este fie algebric, fie transcendental.
o Ansamblul numerelor iraționale este peste tot dens pe linia numerică: există un număr irațional între oricare două numere.
o Setul de numere iraționale este de nenumărat, este un set din a doua categorie Baire.
o Acest set este ordonat, adică pentru fiecare două numere raționale diferite a și b, puteți indica care dintre ele este mai mică decât cealaltă.
o Între fiecare două numere raționale diferite există cel puțin încă un număr rațional și, prin urmare, un set infinit de numere raționale.
o Operațiile aritmetice (adunare, scădere, înmulțire și divizare) pe oricare două numere raționale sunt întotdeauna posibile și duc la un anumit număr rațional. O excepție este împărțirea la zero, ceea ce nu este posibil.
o Fiecare număr rațional poate fi reprezentat ca o fracție zecimală (periodică finită sau infinită).