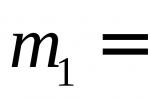Om rationale functies van de vorm R(sin x, cos x) te integreren, wordt een substitutie gebruikt, die de universele trigonometrische substitutie wordt genoemd. Dan . Universele trigonometrische substitutie leidt vaak tot grote berekeningen. Gebruik daarom, waar mogelijk, de volgende vervangingen. ![]()
Integratie van functies die rationeel afhankelijk zijn van trigonometrische functies
1. Integralen van de vorm ∫ sin n xdx , ∫ cos n xdx , n>0a) Als n oneven is, dan moet één macht van sinx (of cosx) onder het teken van het differentieel worden geplaatst, en van de resterende even macht moet men naar de tegenovergestelde functie gaan.
b) Als n even is, gebruiken we de reductieformules
2. Integralen van de vorm ∫ tg n xdx , ∫ ctg n xdx , waarbij n een geheel getal is.
Formules moeten worden gebruikt
3. Integralen van de vorm ∫ sin n x cos m x dx
a) Laat m en n van verschillende pariteit zijn. We passen de substitutie t=sin x toe als n oneven is of t=cos x als m oneven is.
b) Als m en n even zijn, gebruiken we de reductieformules
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integralen van de vorm
Als de getallen m en n dezelfde pariteit hebben, gebruiken we de substitutie t=tg x . Het is vaak handig om de techniek van de trigonometrische eenheid toe te passen.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx
Laten we de formules gebruiken om het product van trigonometrische functies om te zetten in hun som:
- sin α cos β = ½(sin(α+β)+sin(α-β))
- cos α cos β = ½(cos(α+β)+cos(α-β))
- sin α sin β = ½(cos(α-β)-cos(α+β))
Voorbeelden
1. Bereken de integraal ∫ cos 4 x sin 3 xdx .
We maken de substitutie cos(x)=t . Dan ∫ cos 4 x sin 3 xdx = ![]()
![]()
2. Bereken de integraal.
Als we de substitutie sin x=t maken, krijgen we
![]()
3. Zoek de integraal.
We maken de vervanging tg(x)=t . Vervangen, we krijgen
![]()
Integratie van uitdrukkingen van de vorm R(sinx, cosx)
Voorbeeld 1. Bereken integralen: 
Oplossing.
a) Integratie van uitdrukkingen van de vorm R(sinx, cosx) , waarbij R een rationale functie is van sin x en cos x , wordt omgezet in integralen van rationale functies met behulp van de universele trigonometrische substitutie tg(x/2) = t .
Dan hebben we
De universele trigonometrische substitutie maakt het mogelijk om van een integraal van de vorm ∫ R(sinx, cosx) dx over te gaan naar een integraal van een rational-fractionele functie, maar een dergelijke vervanging leidt vaak tot omslachtige uitdrukkingen. Onder bepaalde voorwaarden blijken eenvoudigere substituties effectief:
- Als de gelijkheid R(-sin x, cos x) = -R(sin x, cos x)dx waar is, dan wordt de cos x = t substitutie toegepast.
- Als R(sin x, -cos x) = -R(sin x, cos x)dx waar is, dan is substitutie sin x = t .
- Als R(-sin x, -cos x) = R(sin x, cos x)dx waar is, dan is de substitutie tgx = t of ctg x = t .

we passen de universele trigonometrische substitutie tg(x/2) = t toe.
Antwoord dan:
In de praktijk moet men vaak integralen berekenen van transcendentale functies die goniometrische functies bevatten. In het kader van dit materiaal zullen we de belangrijkste soorten integranden beschrijven en laten zien welke methoden kunnen worden gebruikt om ze te integreren.
Integratie van sinus, cosinus, tangens en cotangens
Laten we beginnen met de methoden voor het integreren van de belangrijkste trigonometrische functies - sin, cos, t g, c t g. Met behulp van de tabel met voorderivaten schrijven we meteen dat ∫ sin x d x \u003d - cos x + C, en ∫ cos x d x \u003d sin x + C.
Om de onbepaalde integralen van de functies t g en c t g te berekenen, kun je de som onder het differentiaalteken gebruiken:
∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C
Hoe hebben we de formules ∫ d x sin x \u003d ln 1 - cos x sin x + C en ∫ d x cos x \u003d ln 1 + sin x cos x + C, overgenomen uit de tabel met voorderivaten? Laten we slechts één geval uitleggen, aangezien het tweede naar analogie duidelijk zal zijn.
Met behulp van de substitutiemethode schrijven we:
∫ d x zonde x = zonde x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2
Hier moeten we de irrationele functie integreren. We gebruiken dezelfde substitutiemethode:
∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 1 - z 2 = ∫ d z z 2 - 1 = ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C
Nu maken we de omgekeerde vervanging z \u003d 1 - t 2 en t \u003d sin x:
∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C
Afzonderlijk zullen we gevallen analyseren met integralen die machten van trigonometrische functies bevatten, zoals ∫ sin n x d x , ∫ cos n x d x , ∫ d x sin n x , ∫ d x cos n x .
Hoe je ze correct berekent, lees je in het artikel over integratie met recursieve formules. Als je weet hoe deze formules zijn afgeleid, dan kun je gemakkelijk integralen als ∫ sin n x cos m x d x nemen met natuurlijk m en n .
Als we een combinatie hebben van goniometrische functies met polynomen of exponentiële functies, dan zullen ze in delen moeten worden geïntegreerd. We raden u aan het artikel te lezen dat gewijd is aan methoden voor het vinden van integralen ∫ P n (x) sin (a x) d x , ∫ P n (x) cos (a x) d x , ∫ e a x sin (a x) d x , ∫ e a x cos (a x ) dx.
Het moeilijkst zijn de problemen waarbij de integrand goniometrische functies met verschillende argumenten bevat. Om dit te doen, moet u de basisformules van trigonometrie gebruiken, dus het is raadzaam om ze uit het hoofd te onthouden of bij de hand te houden.
voorbeeld 1
Zoek de verzameling van antiderivaten van de functie y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) .
Oplossing
We gebruiken de formules voor vermogensreductie en schrijven dat cos 2 x 2 \u003d 1 + cos x 2, en cos 2 2 x \u003d 1 + cos 4 x 2. Middelen,
y = zonde (4 x) + 2 cos 2 (2 x) zonde x cos (3 x) + 2 cos 2 x 2 - 1 zonde (3 x) = zonde (4 x) + 2 1 + cos 4 x 2 zonde x cos (3 x) + 2 1 + cos x 2 - 1 zonde (3 x) = = zonde (4 x) + cos (4 x) + 1 zonde x cos (3 x) + cos x zonde (3 x)
In de noemer hebben we de formule voor de sinus van de som. Dan kun je het zo schrijven:
y = zonde (4 x) + cos (4 x) + 1 zonde x cos (3 x) + cos x zonde (3 x) = zonde (4 x) + cos (4 x) + 1 zonde (4 x ) = = 1 + cos (4 x) zonde (4 x)
We hebben de som van 3 integralen.
∫ sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x ) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C
In sommige gevallen kunnen trigonometrische functies die onder de integraal vallen, worden gereduceerd tot fractioneel rationele uitdrukkingen met behulp van de standaardsubstitutiemethode. Laten we eerst de formules nemen die sin, cos en t g uitdrukken door de raaklijn van een half argument:
sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2
We zullen ook de differentiaal d x moeten uitdrukken in termen van de tangens van de halve hoek:
Sinds d t g x 2 \u003d t g x 2 "d x \u003d d x 2 cos 2 x 2, dan
d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2
Dus, sin x \u003d 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x \u003d 2 d z 1 + z 2 at z \u003d t g x 2.
Voorbeeld 2
Vind de onbepaalde integraal ∫ d x 2 sin x + cos x + 2 .
Oplossing
We gebruiken de standaard trigonometrische substitutiemethode.
2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3
We krijgen dat ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .
Nu kunnen we de integrand uitbreiden tot eenvoudige breuken en de som van twee integralen krijgen:
∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = ln z + 1 - log z + 3 + C = log z + 1 z + 3 + C
∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C
Antwoord: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C
Het is belangrijk op te merken dat die formules die functies uitdrukken in termen van de tangens van een half argument geen identiteiten zijn, daarom is de resulterende uitdrukking ln t g x 2 + 1 t g x 2 + 3 + C de verzameling antiderivaten van de functie y = 1 2 sin x + cos x + 2 alleen op het domein van definitie.
Om andere soorten problemen op te lossen, kunt u de basismethoden van integratie gebruiken.
Als u een fout in de tekst opmerkt, markeer deze dan en druk op Ctrl+Enter
Er zullen ook taken zijn voor een onafhankelijke oplossing, waarop u de antwoorden kunt zien.
De integrand kan worden omgezet van een product van goniometrische functies naar een som
Overweeg integralen waarin de integrand het product is van sinussen en cosinuslijnen van de eerste graad van x vermenigvuldigd met verschillende factoren, dat wil zeggen integralen van de vorm
Met behulp van de bekende trigonometrische formules
(2)
(3)
(4)
men kan elk van de producten in integralen van de vorm (31) omzetten in een algebraïsche som en integreren met de formules
![]() (5)
(5)
![]() (6)
(6)
voorbeeld 1 Vind
![]()
Oplossing. Volgens formule (2) at



Voorbeeld 2 Vind integraal van trigonometrische functie
![]()
Oplossing. Volgens formule (3) at ![]()


![]()
Voorbeeld 3 Vind integraal van trigonometrische functie
![]()
Oplossing. Volgens formule (4) at ![]() krijgen we de volgende transformatie van de integrand:
krijgen we de volgende transformatie van de integrand:

Door formule (6) toe te passen, verkrijgen we:

Integraal van het product van de machten van sinus en cosinus van hetzelfde argument
Laten we nu eens kijken naar de integralen van functies die het product zijn van de machten van de sinus en cosinus van hetzelfde argument, d.w.z.
![]() (7)
(7)
In bepaalde gevallen kan een van de indicatoren ( m of n) kan nul zijn.
Bij het integreren van dergelijke functies wordt gebruikt dat de even macht van de cosinus kan worden uitgedrukt in termen van de sinus, en het differentieel van de sinus is gelijk aan cos x dx(of een even macht van de sinus kan worden uitgedrukt in termen van cosinus, en het cosinusverschil is - sin x dx ) .
Er moeten twee gevallen worden onderscheiden: 1) ten minste één van de indicatoren m en n oneven; 2) beide indicatoren zijn even.
Laat het eerste geval plaatsvinden, namelijk de exponent n = 2k+ 1 - oneven. Dan, gezien dat
![]()

De integrand wordt op zo'n manier gepresenteerd dat het ene deel ervan een functie is van alleen de sinus, en het andere het differentieel van de sinus. Nu met de verandering van variabele t= zonde x de oplossing wordt gereduceerd tot het integreren van de polynoom met betrekking tot t. Als alleen de graad m is vreemd, doe dan hetzelfde, scheid de factor sin x, de rest van de integrand uitdrukken in termen van cos x en ervan uitgaande dat t= cos x. Deze aanpak kan ook worden gebruikt wanneer: integratie van partiële machten van sinus en cosinus , wanneer ten minste één van de indicatoren is vreemd . Het hele punt is dat het quotiënt van de machten van sinus en cosinus is een speciaal geval van hun product : wanneer de goniometrische functie in de noemer van de integrand staat, is de graad negatief. Maar er zijn ook gevallen van partiële goniometrische functies, wanneer hun graden alleen even zijn. Over hen - de volgende paragraaf.
Als beide indicatoren m en n even zijn, gebruik dan goniometrische formules

verlaag de exponenten van de sinus en cosinus, waarna een integraal van hetzelfde type als hierboven wordt verkregen. Daarom moet de integratie op dezelfde manier worden voortgezet. Als een van de even indicatoren negatief is, dat wil zeggen, het quotiënt van de even machten van sinus en cosinus wordt overwogen, dan is dit schema niet geschikt . Vervolgens wordt een verandering van variabele gebruikt, afhankelijk van hoe de integrand kan worden getransformeerd. Een dergelijk geval zal in de volgende sectie worden behandeld.
Voorbeeld 4 Vind integraal van trigonometrische functie
![]()
Oplossing. De exponent van de cosinus is oneven. Stel je daarom voor:
t= zonde x(dan dt= cos x dx ). Dan krijgen we

Terugkerend naar de oude variabele, vinden we eindelijk
![]()
Voorbeeld 5 Vind integraal van trigonometrische functie
![]() .
.
Oplossing. De exponent van de cosinus, zoals in het vorige voorbeeld, is oneven, maar meer. Stel je voor
![]()
en verander de variabele t= zonde x(dan dt= cos x dx ). Dan krijgen we

Laten we de haakjes openen
![]() en krijg
en krijg

Terugkerend naar de oude variabele, verkrijgen we de oplossing

Voorbeeld 6 Vind integraal van trigonometrische functie
![]()
Oplossing. De exponenten van sinus en cosinus zijn even. Daarom transformeren we de integrand als volgt:

Dan krijgen we
In de tweede integraal maken we een verandering van variabele, setting t= sin2 x. Dan (1/2)dt= cos2 x dx . Vervolgens,


Eindelijk krijgen we
![]()
De variabele vervangingsmethode gebruiken
Variabele vervangingsmethode: bij het integreren van trigonometrische functies kan het worden gebruikt in gevallen waarin alleen een sinus of alleen een cosinus aanwezig is in de integrand, het product van sinus en cosinus, waarin ofwel sinus of cosinus in de eerste graad is, ook tangens of cotangens als het quotiënt van de even machten van sinus en cosinus van een en hetzelfde argument. In dit geval is het mogelijk om permutaties uit te voeren, niet alleen sin x = t en zonde x = t, maar ook tg x = t en ctg x = t .
Voorbeeld 8 Vind integraal van trigonometrische functie
![]() .
.
Oplossing. Laten we de variabele veranderen: , dan . De resulterende integrand kan eenvoudig worden geïntegreerd via de tabel met integralen:
![]() .
.
![]()
Voorbeeld 9 Vind integraal van trigonometrische functie
Oplossing. Laten we de tangens omzetten in de verhouding van sinus en cosinus:
Laten we de variabele veranderen: , dan . De resulterende integrand is tabel integraal met minteken:
![]() .
.
Terugkerend naar de oorspronkelijke variabele, krijgen we uiteindelijk:
![]() .
.
Voorbeeld 10 Vind integraal van trigonometrische functie
Oplossing. Laten we de variabele veranderen: , dan .
We transformeren de integrand om de trigonometrische identiteit toe te passen ![]() :
:
We veranderen de variabele, en niet te vergeten een minteken voor de integraal te zetten (zie hierboven, wat gelijk is aan dt). Vervolgens ontleden we de integrand in factoren en integreren we volgens de tabel:
Terugkerend naar de oorspronkelijke variabele, krijgen we uiteindelijk:
![]() .
.
Zoek zelf de integraal van de trigonometrische functie en bekijk de oplossing
Universele trigonometrische substitutie
Universele trigonometrische substitutie kan worden gebruikt in gevallen waarin de integrand niet valt onder de gevallen die in de vorige paragrafen zijn besproken. In principe wanneer de sinus of cosinus (of beide) in de noemer van een breuk staat. Het is bewezen dat de sinus en cosinus als volgt kunnen worden vervangen door een andere uitdrukking die de tangens van de helft van de oorspronkelijke hoek bevat:
Maar merk op dat de universele trigonometrische substitutie vaak nogal complexe algebraïsche transformaties met zich meebrengt, dus het kan het beste worden gebruikt als geen enkele andere methode werkt. Laten we eens kijken naar voorbeelden waarin, samen met de universele trigonometrische substitutie, substitutie onder het teken van het differentieel en de methode van onbepaalde coëfficiënten worden gebruikt.
Voorbeeld 12. Vind integraal van trigonometrische functie
![]() .
.
Oplossing. Oplossing. Laten we gebruiken universele trigonometrische substitutie. Dan  .
.
We vermenigvuldigen de breuken in de teller en de noemer met , en halen de twee eruit en zetten deze voor het integraalteken. Dan
Voorbeelden van oplossingen van integralen door delen worden in detail beschouwd, waarvan de integrand het product is van een polynoom en een exponentiële (e tot de macht van x) of een sinus (sin x) of een cosinus (cos x).
InhoudZie ook: Methode van integratie per onderdelen
Tabel onbepaalde integralen
Methoden voor het berekenen van onbepaalde integralen
Elementaire basisfuncties en hun eigenschappen
Integratie op onderdelen formule
Bij het oplossen van de voorbeelden in deze sectie wordt de formule voor partiële integratie gebruikt:
;
.
Voorbeelden van integralen met het product van een polynoom en sin x, cos x of e x
Hier zijn voorbeelden van dergelijke integralen:
, , .
Om dergelijke integralen te integreren, wordt de polynoom aangegeven met u en de rest met v dx . Vervolgens wordt de partiële integratie-formule toegepast.
Hieronder vindt u een gedetailleerde oplossing van deze voorbeelden.
Voorbeelden van het oplossen van integralen
Voorbeeld met exponent, e tot de macht van x
Definieer integraal:
.
We introduceren de exponent onder het differentiaalteken:
e - x dx = - e - x d(-x) = - d(e - x).
We integreren in delen.
hier
.
De resterende integraal is ook deelbaar.
.
.
.
Eindelijk hebben we:
.
Een voorbeeld van het definiëren van een integraal met een sinus
Bereken integraal:
.
We introduceren de sinus onder het teken van het differentieel:
We integreren in delen.
hier u = x 2 , v = cos(2x+3), du = (
x2 )′
dx
De resterende integraal is ook deelbaar. Om dit te doen, introduceren we de cosinus onder het teken van het differentieel.
hier u = x, v = zonde (2x+3), du = dx
Eindelijk hebben we:
Een voorbeeld van het product van een polynoom en cosinus
Bereken integraal:
.
We introduceren de cosinus onder het teken van het differentieel:
We integreren in delen.
hier u = x 2+3x+5, v = sin2x, du = (
x 2 + 3 x + 5 )′
dx
Basis trigonometrische formules en basissubstituties worden gepresenteerd. Methoden voor het integreren van trigonometrische functies worden geschetst - integratie van rationale functies, product van machtsfuncties van sin x en cos x, product van een polynoom, exponent en sinus of cosinus, integratie van inverse trigonometrische functies. Niet-standaard methoden beïnvloed.
InhoudStandaardmethoden voor het integreren van trigonometrische functies
Algemene benadering
Eerst moet, indien nodig, de integrand worden getransformeerd zodat de trigonometrische functies afhankelijk zijn van één argument, dat zou samenvallen met de integratievariabele.
Als de integrand bijvoorbeeld afhangt van zonde(x+a) en cos(x+b), dan moet u de transformatie uitvoeren:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (ba) + zonde(x+a) zonde(b-a).
Breng vervolgens de wijziging z = x+a aan. Als resultaat zullen de trigonometrische functies alleen afhangen van de integratievariabele z .
Wanneer trigonometrische functies afhankelijk zijn van één argument, samenvallend met de integratievariabele (laten we zeggen dat dit z is), dat wil zeggen, de integrand bestaat alleen uit functies van het type zonde z,
want zo,
tgz,
ctgz, dan moet je een vervanging maken
.
Een dergelijke substitutie leidt tot de integratie van rationele of irrationele functies (als er wortels zijn) en maakt het mogelijk om de integraal te berekenen als deze is geïntegreerd in elementaire functies.
U kunt echter vaak andere methoden vinden waarmee u de integraal op een kortere manier kunt berekenen, op basis van de specifieke kenmerken van de integrand. Hieronder vindt u een samenvatting van de belangrijkste van dergelijke methoden.
Methoden voor het integreren van rationale functies van sin x en cos x
Rationele functies van zonde x en want x zijn functies afgeleid van zonde x,
want x en alle constanten met behulp van de bewerkingen optellen, aftrekken, vermenigvuldigen, delen en verheffen tot een geheel getal. Ze worden als volgt aangeduid: R (sinx, cosx). Dit kan ook raaklijnen en cotangenten omvatten, omdat ze worden gevormd door een sinus te delen door een cosinus en omgekeerd.
Integralen van rationale functies hebben de vorm:
.
Methoden voor het integreren van rationale trigonometrische functies zijn als volgt.
1) Substitutie leidt altijd tot een integraal van een rationale breuk. In sommige gevallen zijn er echter substituties (zie hieronder) die resulteren in kortere berekeningen.
2) Als R (sinx, cosx) cos x → - cos x zonde x.
3) Als R (sinx, cosx) vermenigvuldigd met -1 bij vervanging zonde x → - zonde x, dan is de substitutie t = want x.
4) Als R (sinx, cosx) verandert niet zoals bij gelijktijdige vervanging cos x → - cos x, en zonde x → - zonde x, dan is de substitutie t = tg x of t= ctg x.
Voorbeelden:
,
,
.
Product van machtsfuncties van cos x en sin x
Integralen van de vorm
zijn integralen van rationale trigonometrische functies. Daarom kunnen de methoden die in de vorige sectie zijn beschreven, op hen worden toegepast. Hieronder beschouwen we methoden die zijn gebaseerd op de specifieke kenmerken van dergelijke integralen.
Als m en n rationale getallen zijn, dan is een van de permutaties t = zonde x of t= want x de integraal reduceert tot de integraal van de differentiële binomiaal.
Als m en n gehele getallen zijn, dan wordt de integratie uitgevoerd met behulp van de reductieformules:
;
;
;
.
Voorbeeld:
.
Integralen van het product van een polynoom en een sinus of cosinus
Integralen van de vorm:
,
,
waarbij P(x) een polynoom is in x zijn geïntegreerd door delen. Dit resulteert in de volgende formules:
;
.
Voorbeelden:
,
.
Integralen van het product van een polynoom, exponent en sinus of cosinus
Integralen van de vorm:
,
,
waarbij P(x) een polynoom is in x , worden geïntegreerd met behulp van de Euler-formule
e iax = cos ax + isin ax(waar ik 2 = - 1
).
Hiervoor berekent de in de vorige paragraaf beschreven methode de integraal
.
Nadat de reële en imaginaire delen van het resultaat zijn gescheiden, worden de oorspronkelijke integralen verkregen.
Voorbeeld:
.
Niet-standaard methoden voor het integreren van trigonometrische functies
Hieronder vindt u een aantal niet-standaard methoden waarmee u de integratie van trigonometrische functies kunt uitvoeren of vereenvoudigen.
Afhankelijkheid van (a sin x + b cos x)
Als de integrand alleen afhangt van a zonde x + b cos x, is het handig om de formule toe te passen:
,
waar .
Bijvoorbeeld
Ontleding van breuken van sinussen en cosinus in eenvoudiger breuken
Overweeg de integraal
.
De eenvoudigste manier om te integreren is om de breuk op te splitsen in eenvoudigere, door de transformatie toe te passen:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) zonde(x+b)
Integratie van breuken van de eerste graad
Bij het berekenen van de integraal
,
het is handig om het gehele deel van de breuk en de afgeleide van de noemer te selecteren
a 1 zonde x + b 1 cos x = EEN (a zonde x + b cos x) + B (a zonde x + b cos x)′ .
De constanten A en B worden gevonden door de linker- en rechterkant te vergelijken.
Referenties:
NM Gunther, RO Kuzmin, Verzameling van problemen in de hogere wiskunde, Lan, 2003.