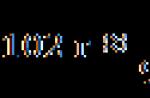Problem je formuliran na sljedeći način: neka željena količina z određuje se preko drugih veličina a, b, c, ... dobivenih izravnim mjerenjima

z = f (a, b, c,...) (1.11)

Potrebno je pronaći srednju vrijednost funkcije i pogrešku njezina mjerenja, tj. pronaći interval pouzdanosti

s pouzdanošću a i relativnom greškom.

Što se tiče, nalazi se zamjenom u desnu stranu (11) umjesto a, b, c,...njihove prosječne vrijednosti

3. Procijenite poluširinu intervala pouzdanosti za rezultat neizravnih mjerenja

,

gdje se derivati... izračunavaju na

4. Odredite relativnu pogrešku rezultata

5. Ako je ovisnost z o a, b, c,... ima oblik , Gdje k, l, m‒ sve realne brojeve, onda prvo morate pronaći relativna greška

i onda apsolutni .

6. Upišite konačni rezultat u obrazac

z = ± Dz, ε = …% na a = … .

Bilješka:

Prilikom obrade rezultata izravnih mjerenja morate se pridržavati sljedećeg pravila: numeričke vrijednosti svih izračunatih veličina moraju sadržavati jednu znamenku više od izvornih (eksperimentalno utvrđenih) veličina.

Za neizravna mjerenja izračuni se rade prema pravila približnih izračuna:

Pravilo 1. Prilikom zbrajanja i oduzimanja približnih brojeva morate:

a) odaberite pojam u kojem sumnjiva znamenka ima najveću znamenku;

b) zaokružite sve ostale članove na sljedeću znamenku (jedna rezervna znamenka se zadržava);

c) vršiti zbrajanje (oduzimanje);

d) kao rezultat, odbacite posljednju znamenku zaokruživanjem (znamenka sumnjive znamenke rezultata podudara se s najvišom od znamenki sumnjivih znamenki izraza).

Primjer: 5,4382·10 5 – 2,918·10 3 + 35,8 + 0,064.

U tim su brojevima zadnje značajne znamenke sumnjive (netočne su već odbačene). Zapišimo ih u obliku 543820 – 2918 + 35,8 + 0,064.

Vidi se da u prvom članu dvojbeni broj 2 ima najveću znamenku (desetice). Zaokruživanjem svih ostalih brojeva na sljedeću znamenku i zbrajanjem dobivamo

543820 – 2918 + 36 + 0 = 540940 = 5,4094 10 5.

Pravilo 2. Prilikom množenja (dijeljenja) približnih brojeva morate:

a) odaberite broj(eve) s najmanjim brojem značajnih znamenki ( ZNAČAJNI – brojevi različiti od nule i nule između njih);

b) zaokružite preostale brojeve tako da imaju jednu značajniju znamenku više (jedna rezervna znamenka se zadržava) od onih dodijeljenih u koraku a;

c) dobivene brojeve pomnožiti (podijeliti);

d) kao rezultat, ostavite onoliko značajnih znamenki koliko ih je bilo u broju(ovima) s najmanjim brojem značajnih znamenki.

Primjer: .

Pravilo 3. Kada se podigne na potenciju, prilikom izvlačenja korijena, rezultat zadržava onoliko značajnih znamenki koliko ih ima u izvornom broju.

Primjer: .

Pravilo 4. Kada se nalazi logaritam broja, mantisa logaritma mora imati onoliko značajnih znamenki koliko ih ima u izvornom broju:

Primjer: .

U završnoj snimci apsolutni pogreške treba ostaviti samo jednu značajnu figuru. (Ako se ispostavi da je ova znamenka 1, tada se nakon nje pohranjuje druga znamenka).

Prosječna vrijednost se zaokružuje na istu znamenku kao i apsolutna pogreška.

Na primjer: V= (375,21 0,03) cm 3 = (3,7521 0,0003) cm 3.

ja= (5,530 0,013) A, A = J.

Radni nalog

Određivanje promjera cilindra.

1. Pomoću čeljusti izmjerite promjer cilindra 7 puta (na različitim mjestima i u različitim smjerovima). Zabilježite rezultate u tablicu.

Ne.

d i, mm

d i-

(d i- ) 2

h i, mm I Povezane informacije:

Pogreške u izmjerenim i tabelarnim veličinama određuju pogreške DH avg neizravno određene vrijednosti, a najveći doprinos DH avg daju najmanje točne vrijednosti, koje imaju najveću relativnu pogrešku d. Stoga je za povećanje točnosti neizravnih mjerenja potrebno postići jednaku točnost izravnih mjerenja.

(d A, d B, d C, ...).

Pravila za pronalaženje pogrešaka u neizravnim mjerenjima:

1. Nađite prirodni logaritam zadane funkcije

ln(X = f(A,B,C,…));

2. Iz pronađenog prirodnog logaritma zadane funkcije pronaći ukupni diferencijal (po svim varijablama);

3. Predznak diferencijala d zamijeniti predznakom apsolutne pogreške D;

4. Zamijenite sve "minuse" s apsolutnim pogreškama DA, DB, DC, ... "profesionalcima".

Rezultat je formula za najveću relativnu pogrešku d x neizravno izmjerena vrijednost X:

d x = = j (A prosj., B prosj., C prosj., ..., DA prosj., DB prosj., DC prosj., ...).(18)

Prema pronađenoj relativnoj pogrešci d x odrediti apsolutnu pogrešku neizravnog mjerenja:

DX av = d x. X prosj . (19)

Rezultat neizravnih mjerenja napisan je u standardnom obliku i prikazan na numeričkoj osi:

X = (X prosj. ± DH prosj.), jedinica. (20)

Primjer:

Odredite vrijednosti relativne i prosječne pogreške fizičke veličine L, neizravno određeno formulom:

, (21)

Gdje π, g, t, k, α, β– veličine čije su vrijednosti izmjerene ili preuzete iz referentnih tablica i unesene u tablicu rezultata mjerenja i tabelarnih podataka (slično tablici 1.).

1. Izračunajte prosječnu vrijednost L prosj, zamjenjujući prosječne vrijednosti iz tablice u (21) – π avg, g avg, t avg, k avg, α avg, β avg.

2. Odredite najveću relativnu pogrešku δ L:

a). Formula logaritma (21):

b). Rezultirajući izraz (22) je diferenciran:

c) Zamijenite predznak diferencijala d s Δ, a “minuse” ispred apsolutnih pogrešaka s “plusovima” i tako dobijete izraz za najveću relativnu pogrešku. δ L:

d). Zamjenom prosječnih vrijednosti ulaznih veličina i njihovih pogrešaka iz tablice rezultata mjerenja u dobiveni izraz izračunajte δ L.

3. Zatim izračunajte apsolutnu pogrešku ΔL prosj:

Rezultat se bilježi u standardnom obliku i grafički prikazuje na osi L:

, jedinice promijeniti

ELEMENTARNE PROCJENE POGREŠKE MJERENJA

Mjerenje je pronalaženje vrijednosti fizikalne veličine eksperimentalnim putem uz pomoć posebnih tehničkih sredstava – mjera, mjernih instrumenata.

Mjera je mjerno sredstvo koje reproducira fizikalnu veličinu zadane veličine – mjernu jedinicu, njezinu višestruku ili razlomačku vrijednost. Na primjer, utezi 1 kg, 5 kg, 10 kg.

Mjerni uređaj je mjerni instrument dizajniran za generiranje signala mjerne informacije u obliku koji je dostupan promatraču izravnom percepcijom. Mjerni uređaj omogućuje izravnu ili neizravnu usporedbu izmjerene vrijednosti s mjerama. Mjerenja se također dijele na izravna i neizravna.

Kod izravnih mjerenja željena vrijednost veličine nalazi se izravno iz osnovnih (eksperimentalnih) podataka.

Kod neizravnih mjerenja željena vrijednost veličine nalazi se na temelju poznatog odnosa između te veličine i veličina koje su podvrgnute izravnim mjerenjima. Princip mjerenja je skup fizikalnih pojava na kojima se temelje mjerenja.

Metoda mjerenja je skup tehnika za korištenje principa i mjernih instrumenata. Vrijednost fizikalne veličine, koja bi idealno odražavala u kvalitativnom i kvantitativnom smislu odgovarajuće svojstvo danog objekta, je prava vrijednost fizikalne veličine. Vrijednost fizikalne veličine dobivena njezinim mjerenjem je rezultat mjerenja.

Odstupanje rezultata mjerenja od stvarne vrijednosti izmjerene veličine je greška mjerenja.

Apsolutna mjerna pogreška je mjerna pogreška, izražena u jedinicama izmjerene veličine i jednaka razlici između rezultata i prave vrijednosti izmjerene veličine. Omjer apsolutne greške i stvarne vrijednosti mjerene veličine je relativna greška mjerenja.

Doprinosi pogrešci mjerenja uključuju pogreške mjernih instrumenata (pogreška instrumenta ili instrumenta), nesavršenost mjerne metode, pogrešku očitanja na skali instrumenta, vanjske utjecaje na sredstva i objekte mjerenja te kašnjenje ljudske reakcije na svjetlosne i zvučne signale. .

Po prirodi manifestacije pogreške se dijele na sustavne i slučajne. Slučajni događaj je događaj koji se, s obzirom na određeni skup faktora, može, ali i ne mora dogoditi.

Slučajna pogreška je komponenta mjerne pogreške koja se nasumično mijenja s ponavljanjem mjerenja iste veličine. Karakteristična značajka slučajnih pogrešaka je promjena veličine i predznaka pogreške pri stalnim uvjetima mjerenja.

Sustavna pogreška je komponenta mjerne pogreške koja ostaje konstantna ili se prirodno mijenja s ponavljanjem mjerenja iste veličine. Sustavne pogreške se, u načelu, mogu otkloniti korekcijama i primjenom preciznijih instrumenata i metoda (iako u praksi sustavne pogreške nije uvijek lako otkriti). Nemoguće je isključiti slučajne pogreške u pojedinačnim mjerenjima; matematička teorija slučajnih pojava (teorija vjerojatnosti) omogućuje samo uspostavljanje razumne procjene njihove veličine.

Pogreške izravnih mjerenja

Pretpostavimo da su sustavne pogreške isključene i da su pogreške u rezultatima mjerenja samo slučajne. Označimo slovima rezultate mjerenja fizičke veličine čija je prava vrijednost jednaka . Navedene su apsolutne pogreške rezultata pojedinačnih mjerenja:

Zbrajajući lijevu i desnu stranu jednakosti (1), dobivamo:

(2)

Teorija slučajnih pogrešaka temelji se na pretpostavkama potvrđenim iskustvom:

pogreške mogu poprimiti kontinuirani niz vrijednosti;

kod velikog broja mjerenja jednako se često javljaju slučajne pogreške iste veličine, ali različitih predznaka;

vjerojatnost pogreške opada kako se njezina veličina povećava. Također je potrebno da pogreške budu male u odnosu na izmjerenu vrijednost i neovisne.

Prema pretpostavci (1) s brojem mjerenja n   dobivamo

,

Međutim, broj dimenzija je uvijek konačan i ostaje nepoznato. Ali za praktične svrhe, dovoljno je eksperimentalno pronaći vrijednost fizičke veličine toliko blizu prave da može se koristiti umjesto true. Pitanje je kako ocijeniti stupanj te aproksimacije?

Prema teoriji vjerojatnosti, aritmetička sredina niza mjerenja pouzdaniji od rezultata pojedinačnih mjerenja, jer slučajna odstupanja od prave vrijednosti u različitim smjerovima jednako su vjerojatna. Vjerojatnost pojavljivanja vrijednosti a i u intervalu širine 2a i shvaća se kao relativna učestalost pojavljivanja vrijednosti a i unutar intervala 2a i prema broju svih pojavnih vrijednosti a i pri čemu broj pokusa (mjerenja) teži beskonačnosti. Očigledno je da je vjerojatnost pouzdanog događaja jednaka jedinici, vjerojatnost nemogućeg događaja jednaka je nuli, tj. 0    100%.

Vjerojatnost da je željena vrijednost (njena prava vrijednost) sadržana u intervalu (a - a, a + a) nazvat ćemo vjerojatnošću povjerenja (pouzdanosti) , a odgovarajući  interval (a - a, a + a) - interval pouzdanosti; Što je pogreška a manja, to je manja vjerojatnost da se izmjerena vrijednost nalazi u intervalu definiranom tom pogreškom. Vrijedi i suprotna tvrdnja: što je rezultat manje pouzdan, to je uži interval pouzdanosti željene vrijednosti.

Za veliko n (praktički za n  100), poluširina intervala pouzdanosti za danu pouzdanost  jednaka je

, (3)

gdje je K() = 1 pri  = 0,68; K() = 2 kod  = 0,95; K() = 3 kod  = 0,997.

Kod malog broja mjerenja, što se najčešće susreće u studentskim laboratorijskim vježbama, koeficijent K() u (3) ne ovisi samo o , već i o broju mjerenja n. Stoga, u prisutnosti samo slučajne pogreške, uvijek ćemo pronaći poluširinu intervala pouzdanosti pomoću formule

(4)

U (4) koeficijent t  n naziva se Studentov koeficijent. Za  = 0,95 usvojene u studentskoj praksi, vrijednosti t  n su sljedeće:

Vrijednost se naziva korijen srednje kvadratne pogreške aritmetičke sredine niza mjerenja.

Pogreška instrumenta ili mjere obično je označena u njegovoj putovnici ili simbolom na skali instrumenta. Obično se pogreška instrumenta  shvaća kao poluširina intervala unutar kojeg se izmjerena vrijednost može zadržati uz vjerojatnost mjerenja od 0,997, ako je pogreška mjerenja posljedica samo pogreške instrumenta. Kao opću (ukupnu) pogrešku rezultata mjerenja prihvatit ćemo s vjerojatnošću  = 0,95

Apsolutna pogreška omogućuje vam da odredite u kojem je znaku dobivenog rezultata sadržana netočnost. Relativna pogreška daje informaciju o tome koji je udio (postotak) izmjerene vrijednosti pogreška (poluširina intervala pouzdanosti).

Konačni rezultat niza izravnih mjerenja vrijednosti a 0 upisujemo u obrazac

.

Na primjer

(6)

Dakle, svaka fizikalna veličina pronađena eksperimentalno mora biti predstavljena:

Neka neka slučajna varijabla a izmjereno n puta pod istim uvjetima. Rezultati mjerenja dali su set n različite brojeve

Apsolutna pogreška- dimenzionalna vrijednost. Među n Apsolutne vrijednosti pogreške su nužno i pozitivne i negativne.

Za najvjerojatnije vrijednosti količine A obično se uzima prosjek vrijednost rezultata mjerenja

.

Što je veći broj mjerenja, to je prosječna vrijednost bliža stvarnoj vrijednosti.

Apsolutna pogreškaja

.

Relativna greškaja-to mjerenje naziva se količina

Relativna greška je bezdimenzijska veličina. Za to se obično relativna pogreška izražava u postocima e i pomnožite sa 100%. Veličina relativne pogreške karakterizira točnost mjerenja.

Prosječna apsolutna greška definira se ovako:

.

Naglašavamo potrebu zbrajanja apsolutnih vrijednosti (modula) veličina D i ja U suprotnom, rezultat će biti identična nula.

Prosječna relativna pogreška naziva se količina

.

Za veliki broj mjerenja.

Relativna pogreška može se smatrati vrijednošću pogreške po jedinici izmjerene vrijednosti.

Točnost mjerenja procjenjuje se usporedbom pogrešaka rezultata mjerenja. Stoga se pogreške mjerenja izražavaju u takvom obliku da je za procjenu točnosti dovoljno usporediti samo pogreške rezultata, bez usporedbe veličina mjernih predmeta ili vrlo približnog poznavanja tih veličina. Iz prakse je poznato da apsolutna pogreška pri mjerenju kuta ne ovisi o vrijednosti kuta, a apsolutna pogreška pri mjerenju duljine ovisi o vrijednosti duljine. Što je duljina veća, to je veća apsolutna pogreška za danu metodu i uvjete mjerenja. Prema tome, apsolutna pogreška rezultata može se koristiti za procjenu točnosti mjerenja kuta, ali se ne može prosuditi točnost mjerenja duljine. Izražavanje pogreške u relativnom obliku omogućuje usporedbu točnosti kutnih i linearnih mjerenja u poznatim slučajevima.

Osnovni pojmovi teorije vjerojatnosti. Slučajna pogreška.

Slučajna pogreška naziva se komponenta pogreške mjerenja koja se nasumično mijenja tijekom ponovljenih mjerenja iste veličine.

Kada se opetovana mjerenja iste konstantne, nepromjenjive veličine provode s istom pažnjom i pod istim uvjetima, dobivamo rezultate mjerenja - neki se međusobno razlikuju, a neki podudaraju. Takva odstupanja u rezultatima mjerenja ukazuju na prisutnost komponenti slučajne pogreške u njima.

Slučajna pogreška proizlazi iz istovremenog utjecaja više izvora, od kojih svaki za sebe ima neprimjetan učinak na rezultat mjerenja, ali ukupni utjecaj svih izvora može biti prilično jak.

Slučajne pogreške su neizbježna posljedica bilo kojeg mjerenja i uzrokuju ih:

a) netočnost očitanja na ljestvici instrumenata i instrumenata;

b) neidentičnost uvjeta za ponovljena mjerenja;

c) slučajne promjene vanjskih uvjeta (temperatura, tlak, polje sila itd.), koje se ne mogu kontrolirati;

d) svi drugi utjecaji na mjerenja, čiji su nam uzroci nepoznati. Veličina slučajne pogreške može se minimizirati ponavljanjem eksperimenta mnogo puta i odgovarajućom matematičkom obradom dobivenih rezultata.

Slučajna pogreška može poprimiti različite apsolutne vrijednosti, koje je nemoguće predvidjeti za određeno mjerenje. Ova greška može biti jednako pozitivna ili negativna. U eksperimentu su uvijek prisutne slučajne pogreške. U nedostatku sustavnih pogrešaka, one uzrokuju raspršenost ponovljenih mjerenja u odnosu na pravu vrijednost.

Pretpostavimo da se period titranja njihala mjeri štopericom i da se mjerenje ponavlja mnogo puta. Pogreške u pokretanju i zaustavljanju štoperice, pogreška u očitanoj vrijednosti, mala neravnomjernost u kretanju njihala - sve to uzrokuje raspršivanje rezultata ponovljenih mjerenja i stoga se može klasificirati kao slučajne pogreške.

Ako nema drugih pogrešaka, tada će neki rezultati biti donekle precijenjeni, dok će drugi biti donekle podcijenjeni. Ali ako uz to još i sat zaostane, onda će svi rezultati biti podcijenjeni. To je već sustavna greška.

Neki čimbenici mogu uzrokovati i sustavne i slučajne pogreške u isto vrijeme. Dakle, uključivanjem i isključivanjem štoperice, možemo stvoriti malu nepravilnu razliku u vremenima početka i zaustavljanja sata u odnosu na kretanje njihala i time unijeti slučajnu pogrešku. Ali ako, osim toga, svaki put žurimo uključiti štopericu i malo kasnimo da je isključimo, tada će to dovesti do sustavne pogreške.

Slučajne pogreške uzrokovane su pogreškom paralakse pri brojanju podjeljaka instrumenta, podrhtavanjem temelja zgrade, utjecajem laganog kretanja zraka itd.

Iako je nemoguće eliminirati slučajne pogreške u pojedinačnim mjerenjima, matematička teorija slučajnih pojava omogućuje smanjenje utjecaja tih pogrešaka na konačni rezultat mjerenja. U nastavku će se pokazati da je za to potrebno napraviti ne jedno, već više mjerenja, a što je manja vrijednost pogreške koju želimo dobiti, potrebno je napraviti više mjerenja.

Zbog činjenice da je pojava slučajnih pogrešaka neizbježna i neizbježna, glavni zadatak svakog mjernog procesa je svesti pogreške na najmanju moguću mjeru.

Teorija pogrešaka temelji se na dvije glavne pretpostavke, potvrđene iskustvom:

1. Kod velikog broja mjerenja često se javljaju slučajne pogreške iste veličine, ali različitih predznaka, odnosno pogreške u smjeru povećanja i smanjenja rezultata.

2. Pogreške koje su velike u apsolutnoj vrijednosti rjeđe su od malih, stoga se vjerojatnost pojave pogreške smanjuje kako se njezina veličina povećava.

Ponašanje slučajnih varijabli opisuje se statističkim obrascima, koji su predmet teorije vjerojatnosti. Statistička definicija vjerojatnosti w i događanja ja je odnos

Gdje n- ukupan broj eksperimenata, n i- broj eksperimenata u kojima je događaj ja dogodilo se. U tom slučaju, ukupan broj eksperimenata trebao bi biti vrlo velik ( n®¥). Kod velikog broja mjerenja, slučajne pogreške podliježu normalnoj distribuciji (Gaussova distribucija), čije su glavne značajke sljedeće:

1. Što je veće odstupanje izmjerene vrijednosti od prave vrijednosti, manja je vjerojatnost za takav rezultat.

2. Odstupanja u oba smjera od prave vrijednosti jednako su vjerojatna.

Iz navedenih pretpostavki proizlazi da je za smanjenje utjecaja slučajnih pogrešaka potrebno izmjeriti ovu vrijednost nekoliko puta. Pretpostavimo da mjerimo neku količinu x. Neka se proizvodi n mjerenja: x 1, x 2, ... x n- koristeći istu metodu i s istom pažnjom. Može se očekivati ​​da broj dn dobiveni rezultati, koji leže u nekom prilično uskom intervalu od x prije x + dx, mora biti proporcionalan:

Veličina uzetog intervala dx;

Ukupan broj mjerenja n.

Vjerojatnost dw(x) da neka vrijednost x leži u rasponu od x prije x + dx, je definiran na sljedeći način :

(sa brojem mjerenja n ®¥).

Funkcija f(x) naziva se funkcija distribucije ili gustoća vjerojatnosti.

Kao postulat teorije pogrešaka prihvaćeno je da se rezultati izravnih mjerenja i njihove slučajne pogreške, kada ih je mnogo, pokoravaju zakonu normalne raspodjele.

Funkcija distribucije kontinuirane slučajne varijable koju je pronašao Gauss x ima sljedeći oblik:

, gdje mis - parametri distribucije .

Parametar m normalne distribucije jednak je srednjoj vrijednosti b x– slučajna varijabla, koja je za proizvoljno poznatu funkciju raspodjele određena integralom

.

Tako, vrijednost m je najvjerojatnija vrijednost mjerene veličine x, tj. njezina najbolja procjena.

Parametar s 2 normalne distribucije jednak je varijanci D slučajne varijable, koja je u općem slučaju određena sljedećim integralom

.

Kvadratni korijen varijance naziva se standardna devijacija slučajne varijable.

Prosječno odstupanje (pogreška) slučajne varijable ásñ određuje se pomoću funkcije distribucije kako slijedi

Prosječna pogreška mjerenja ásñ, izračunata iz Gaussove funkcije distribucije, povezana je s vrijednošću standardne devijacije s na sljedeći način:

< s > = 0,8 s.

Parametri s i m međusobno su povezani na sljedeći način:

.

Ovaj izraz vam omogućuje da pronađete standardnu ​​devijaciju s ako postoji krivulja normalne distribucije.

Na slikama je prikazan graf Gaussove funkcije. Funkcija f(x) je simetrična u odnosu na ordinatu povučenu u točki x = m; prolazi kroz maksimum u točki x = m i ima infleksiju u točkama m ±s. Dakle, varijanca karakterizira širinu funkcije distribucije ili pokazuje koliko su vrijednosti slučajne varijable raspršene u odnosu na njezinu pravu vrijednost. Što su mjerenja točnija, to su rezultati pojedinih mjerenja bliži stvarnoj vrijednosti, tj. vrijednost s je manja. Slika A prikazuje funkciju f(x) za tri vrijednosti s .

Područje figure okruženo krivuljom f(x) i okomite crte povučene iz točaka x 1 i x 2 (slika B) , brojčano jednaka vjerojatnosti da rezultat mjerenja padne u interval D x = x 1 - x 2, koja se naziva vjerojatnost povjerenja. Područje ispod cijele krivulje f(x) jednaka je vjerojatnosti da slučajna varijabla padne u interval od 0 do ¥, tj.

,

budući da je vjerojatnost pouzdanog događaja jednaka jedinici.

Koristeći normalnu distribuciju, teorija pogrešaka postavlja i rješava dva glavna problema. Prvi je procjena točnosti obavljenih mjerenja. Drugi je procjena točnosti aritmetičke sredine rezultata mjerenja.5. Interval pouzdanosti. Koeficijent učenika.

Teorija vjerojatnosti omogućuje nam da odredimo veličinu intervala u kojem, uz poznatu vjerojatnost w nalaze se rezultati pojedinih mjerenja. Ova vjerojatnost se zove povjerenje vjerojatnost, i odgovarajući interval (<x>±D x)w nazvao interval pouzdanosti. Vjerojatnost pouzdanosti također je jednaka relativnom udjelu rezultata koji spadaju unutar intervala pouzdanosti.

Ako je broj mjerenja n je dovoljno velika, tada vjerojatnost pouzdanja izražava udio ukupnog broja n ona mjerenja u kojima je izmjerena vrijednost bila unutar intervala pouzdanosti. Svaka vjerojatnost povjerenja w odgovara njegovom intervalu pouzdanosti.w 2 80%. Što je širi interval pouzdanosti, to je veća vjerojatnost dobivanja rezultata unutar tog intervala. U teoriji vjerojatnosti uspostavlja se kvantitativni odnos između vrijednosti intervala pouzdanosti, vjerojatnosti pouzdanosti i broja mjerenja.

Odaberemo li kao interval pouzdanosti interval koji odgovara prosječnoj pogrešci, tj. D a = oglas Añ, tada za dovoljno velik broj mjerenja odgovara vjerojatnosti povjerenja w 60%. Kako se broj mjerenja smanjuje, vjerojatnost pouzdanosti koja odgovara takvom intervalu pouzdanosti (á Añ ± oglas Añ), smanjuje.

Dakle, za procjenu intervala pouzdanosti slučajne varijable, može se koristiti vrijednost prosječne pogreške áD Añ .

Za karakterizaciju veličine slučajne pogreške potrebno je navesti dva broja, naime vrijednost intervala pouzdanosti i vrijednost vjerojatnosti pouzdanosti . Navođenje samo veličine pogreške bez odgovarajuće vjerojatnosti pouzdanosti uglavnom je besmisleno.

Ako je poznata prosječna pogreška mjerenja ásñ, interval pouzdanosti zapisan kao (<x> ± ásñ) w, određeno s vjerojatnošću povjerenja w= 0,57.

Ako je poznata standardna devijacija s raspodjele rezultata mjerenja navedeni interval ima oblik (<x>± t w s) w, Gdje t w- koeficijent koji ovisi o vrijednosti vjerojatnosti pouzdanosti i izračunava se pomoću Gaussove distribucije.

Najčešće korištene količine D x dati su u tabeli 1.

Rezultat mjerenja neke fizikalne veličine uvijek se razlikuje od stvarne vrijednosti za određeni iznos, koji se naziva greška

KLASIFIKACIJA:

1. Po načinu izražavanja: apsolutni, reducirani i relativni

2. Prema izvoru nastanka: metodološki i instrumentalni.

3. Prema uvjetima i uzrocima nastanka: glavni i dodatni

4. Po prirodi promjena: sustavne i slučajne.

5. Ovisno o ulaznoj mjernoj veličini: aditivna i multiplikativna

6. Ovisno o tromosti: statički i dinamički.

13. Apsolutne, relativne i reducirane pogreške.

Apsolutna pogreška je razlika između izmjerene i stvarne vrijednosti izmjerene veličine:

gdje je A izmjereno, A je izmjerena i stvarna vrijednost; ΔA - apsolutna pogreška.

Apsolutna pogreška izražava se u jedinicama izmjerene vrijednosti. Apsolutna pogreška uzeta sa suprotnim predznakom naziva se korekcija.

Relativnigreška p je jednak omjeru apsolutne pogreške ΔA prema stvarnoj vrijednosti izmjerene vrijednosti i izražava se kao postotak:

S obziromgreška mjerila je omjer apsolutne pogreške i nazivne vrijednosti. Nazivna vrijednost za uređaj s jednostranom ljestvicom jednaka je gornjoj granici mjerenja, za uređaj s dvostranom ljestvicom (s nulom u sredini) - aritmetičkom zbroju gornjih granica mjerenja:

pr.br.

14. Metodološke, instrumentalne, sustavne i slučajne pogreške.

Greška metode je zbog nesavršenosti korištene metode mjerenja, netočnosti formula i matematičkih ovisnosti koje opisuju ovu metodu mjerenja, kao i utjecaja mjernog instrumenta na objekt čija se svojstva mijenjaju.

Instrumentalna greška(pogreška instrumenta) je zbog konstrukcijskih značajki mjernog uređaja, netočnosti kalibracije i ljestvice, kao i neispravne ugradnje mjernog uređaja.

Instrumentalna pogreška, u pravilu, naznačena je u putovnici za mjerni instrument i može se procijeniti numerički.

Sustavna pogreška- konstantna ili prirodno promjenjiva pogreška tijekom ponovljenih mjerenja iste veličine pod istim uvjetima mjerenja. Na primjer, pogreška koja se javlja pri mjerenju otpora amper-voltmetrom uzrokovana je slabom baterijom.

Slučajna pogreška- pogreška mjerenja, čija se priroda mijenja tijekom ponovljenih mjerenja iste količine pod istim uvjetima je slučajna. Na primjer, pogreška brojanja tijekom nekoliko ponovljenih mjerenja.

Uzrok slučajne pogreške je istovremeno djelovanje mnogih slučajnih čimbenika, od kojih svaki pojedinačno ima mali učinak.

Slučajnu pogrešku moguće je procijeniti i djelomično smanjiti pravilnom obradom metodama matematičke statistike, kao i metodama vjerojatnosti.

15. Osnovne i dodatne, statičke i dinamičke pogreške.

Osnovna pogreška- pogreška koja se javlja u normalnim uvjetima uporabe mjerila (temperatura, vlaga, napon napajanja i dr.), koji su standardizirani i navedeni u normama ili tehničkim specifikacijama.

Dodatna greška uzrokovana je odstupanjem jedne ili više utjecajnih veličina od normalne vrijednosti. Na primjer, promjene u temperaturi okoline, promjene u vlažnosti, fluktuacije u naponu napajanja. Vrijednost dodatne pogreške normirana je i navedena u tehničkoj dokumentaciji za mjerila.

Statička greška- pogreška pri mjerenju vremenski konstantne vrijednosti. Na primjer, pogreška mjerenja konstantnog strujnog napona tijekom mjerenja.

Dinamička pogreška- pogreška mjerenja vremenski promjenjive veličine. Na primjer, greška u mjerenju komutiranog istosmjernog napona, uzrokovana prijelaznim procesima tijekom komutacije, kao i ograničena brzina mjernog uređaja.

3.1 Pogreška aritmetičke sredine. Kao što je ranije navedeno, mjerenja u osnovi ne mogu biti apsolutno točna. Stoga se tijekom mjerenja postavlja zadatak određivanja intervala u kojem se najvjerojatnije nalazi prava vrijednost izmjerene vrijednosti. Ovaj interval je naznačen u obliku apsolutne pogreške mjerenja.

Ako pretpostavimo da su grube pogreške u mjerenjima eliminirane, a sustavne pogreške pomnim podešavanjem instrumenata i cijele instalacije minimizirane i nisu odlučujuće, tada će rezultati mjerenja uglavnom sadržavati samo slučajne pogreške, a to su naizmjenične veličine. Dakle, ako se provodi više ponovljenih mjerenja iste veličine, tada je najvjerojatnija vrijednost izmjerene veličine njezina aritmetička sredina:

Prosječna apsolutna greška naziva se aritmetička sredina modula apsolutne pogreške pojedinačnih mjerenja:

Posljednja nejednakost obično se piše kao konačni rezultat mjerenja na sljedeći način:

(5)

pri čemu se apsolutna pogreška a cf mora izračunati (zaokružiti) s točnošću jedne ili dvije značajne brojke. Apsolutna pogreška pokazuje koji predznak broja sadrži netočnosti, dakle u izrazu za srijeda Ostavljaju sve točne brojeve i jedan sumnjiv. To jest, srednja vrijednost i srednja pogreška izmjerene vrijednosti moraju se izračunati na znamenku iste znamenke. Na primjer: g = (9,78 ± 0,24) m/s 2 .

Relativna greška. Apsolutna pogreška određuje interval najvjerojatnijih vrijednosti izmjerene vrijednosti, ali ne karakterizira stupanj točnosti izvršenih mjerenja. Na primjer, udaljenost između naseljenih mjesta, mjerena s točnošću od nekoliko metara, može se svrstati u vrlo precizna mjerenja, dok će mjerenje promjera žice s točnošću od 1 mm u većini slučajeva biti vrlo aproksimativna mjera.

Stupanj točnosti obavljenih mjerenja karakterizira relativna pogreška.

Prosjek relativna pogreška ili jednostavno relativna mjerna pogreška je omjer prosječne apsolutne mjerne pogreške i prosječne vrijednosti izmjerene veličine:

Relativna pogreška je bezdimenzijska veličina i obično se izražava u postocima.

3.2 Pogreška metode ili pogreška instrumenta. Aritmetička srednja vrijednost izmjerene veličine je to bliža stvarnoj što se više mjerenja vrši, dok apsolutna pogreška mjerenja s porastom broja teži vrijednosti koja je određena metodom mjerenja i tehničkim karakteristikama korištenih instrumenata.

Greška metode ili se pogreška instrumenta može izračunati iz jednokratnog mjerenja, znajući klasu točnosti uređaja ili druge podatke u tehničkoj putovnici uređaja, koji označavaju ili klasu točnosti uređaja ili njegovu apsolutnu ili relativnu pogrešku mjerenja.

Klasa točnosti uređaj izražava u postotku nazivnu relativnu pogrešku uređaja, odnosno relativnu pogrešku mjerenja kada je izmjerena vrijednost jednaka graničnoj vrijednosti za određeni uređaj

Apsolutna pogreška uređaja ne ovisi o vrijednosti mjerene veličine.

Relativna greška uređaja (po definiciji):

(10)

iz čega se vidi da je relativna pogreška instrumenta manja što je vrijednost mjerene veličine bliža granici mjerenja danog uređaja. Stoga se preporučuje odabir uređaja tako da izmjerena vrijednost bude 60-90% vrijednosti za koju je uređaj predviđen. Kada radite s instrumentima s više raspona, trebali biste nastojati osigurati da se očitanje vrši u drugoj polovici ljestvice.

Pri radu s jednostavnim instrumentima (ravnalo, čaša, itd.), Točnost i klasa pogreške nisu određene tehničkim karakteristikama, apsolutna pogreška izravnih mjerenja uzima se jednakom polovici vrijednosti podjele ovog instrumenta. (Vrijednost podjeljka je vrijednost mjerene veličine kada su očitanja instrumenta jedan podjeljak).

Pogreška instrumenta neizravnih mjerenja može se izračunati pomoću pravila približnog izračuna. Izračun pogreške neizravnih mjerenja temelji se na dva uvjeta (pretpostavke):

1. Apsolutne pogreške mjerenja uvijek su vrlo male u usporedbi s izmjerenim vrijednostima. Stoga se apsolutne pogreške (u teoriji) mogu smatrati infinitezimalnim priraštajima izmjerenih veličina i mogu se zamijeniti odgovarajućim diferencijalima.

2. Ako je fizikalna veličina, koja se određuje posredno, funkcija jedne ili više izravno mjerenih veličina, tada je i apsolutna pogreška funkcije, zbog infinitezimalnih priraštaja, također beskonačno mala veličina.

Pod ovim pretpostavkama, apsolutne i relativne pogreške mogu se izračunati korištenjem dobro poznatih izraza iz teorije diferencijalnog računa funkcija mnogih varijabli:

	(11)
	(12)

Apsolutne pogreške izravnih mjerenja mogu imati predznak plus ili minus, ali nije poznato koji. Stoga se pri određivanju pogrešaka smatra najnepovoljnijim slučajem kada pogreške u izravnim mjerenjima pojedinih veličina imaju isti predznak, odnosno apsolutna pogreška ima najveću vrijednost. Stoga se pri računanju priraštaja funkcije f(x 1,x 2,…,x n) prema formulama (11) i (12), parcijalni prirasti moraju se dodati u apsolutnoj vrijednosti. Dakle, korištenjem aproksimacije Dh i ≈ dx i, i izraze (11) i (12), za infinitezimalne inkremente Da može se napisati:

	(13)
	(14)

Ovdje: A - neizravno mjerena fizikalna veličina, tj. određena računskom formulom, Da- apsolutna greška njegovog mjerenja, x 1, x 2,...x n; Dh 1, Dx 2,..., Dh n,- fizikalne veličine izravnih mjerenja, odnosno njihove apsolutne pogreške.

Dakle: a) apsolutna pogreška neizravne metode mjerenja jednaka je zbroju apsolutnih vrijednosti proizvoda parcijalnih derivata mjerne funkcije i odgovarajućih apsolutnih pogrešaka izravnih mjerenja; b) relativna pogreška neizravne metode mjerenja jednaka je zbroju diferencijalnih modula iz prirodnog logaritma mjerne funkcije, određenog formulom za izračun.

Izrazi (13) i (14) omogućuju izračunavanje apsolutnih i relativnih pogrešaka na temelju jednokratnog mjerenja. Imajte na umu da je za smanjenje izračuna pomoću ovih formula dovoljno izračunati jednu od pogrešaka (apsolutnu ili relativnu), a drugu izračunati pomoću jednostavnog odnosa između njih:

(15)

U praksi se češće koristi formula (13), budući da se kod logaritmiranja formule za izračun umnošci različitih veličina pretvaraju u odgovarajuće zbrojeve, a potencije i eksponencijalne funkcije u umnoške, što uvelike pojednostavljuje proces diferencijacije. .

Za praktične smjernice za izračunavanje pogreške metode neizravnog mjerenja, možete koristiti sljedeće pravilo:

Za izračun relativne pogreške neizravne metode mjerenja potrebno je:

1. Odredite apsolutne pogreške (instrumentalne ili prosječne) izravnih mjerenja.

2. Logaritmirajte računsku (radnu) formulu.

3. Uzimajući vrijednosti izravnih mjerenja kao neovisne varijable, pronađite ukupni diferencijal dobivenog izraza.

4. Zbrojite sve parcijalne razlike u apsolutnim vrijednostima, zamjenjujući varijable razlike u njima odgovarajućim apsolutnim pogreškama izravnih mjerenja.

Na primjer, gustoća cilindričnog tijela izračunava se po formuli:

(16)

Gdje m, D, h - izmjerene količine.

Dobijmo formulu za izračunavanje pogrešaka.

1. Na temelju korištene opreme utvrđujemo apsolutne pogreške u mjerenju mase, promjera i visine cilindra (∆m, ∆D, ∆h odnosno).

2. Logaritmirajmo izraz (16):

3. Razlikovati:

4. Zamjenom diferencijala nezavisnih varijabli s apsolutnim pogreškama i dodavanjem modula parcijalnih inkremenata dobivamo:

5. Korištenje numeričkih vrijednosti m, D, h, D, m, h, brojimo E.

6. Izračunajte apsolutnu pogrešku

Gdje r izračunato pomoću formule (16).

Predlažemo da se sami uvjerite da je u slučaju šupljeg cilindra ili cijevi s unutarnjim promjerom D 1 i vanjski promjer D 2

Potrebno je pribjeći izračunavanju pogreške metode mjerenja (izravne ili neizravne) u slučajevima kada se višestruka mjerenja ili ne mogu provesti pod istim uvjetima ili zahtijevaju puno vremena.

Ako je određivanje pogreške mjerenja temeljni zadatak, tada se mjerenja obično provode opetovano i izračunavaju se i pogreška aritmetičke sredine i pogreška metode (pogreška instrumenta). Konačni rezultat označava najveći od njih.

O točnosti izračuna

Pogreška u rezultatu određena je ne samo netočnostima mjerenja već i netočnostima izračuna. Izračuni se moraju izvesti tako da je njihova pogreška za red veličine manja od pogreške u rezultatu mjerenja. Da biste to učinili, sjetite se pravila matematičkih operacija s približnim brojevima.

Rezultati mjerenja su približni brojevi. U okvirnom broju svi brojevi moraju biti točni. Posljednjom točnom znamenkom približnog broja smatra se ona u kojoj pogreška ne prelazi jednu jedinicu njegove znamenke. Sve znamenke od 1 do 9 i 0, ako je u sredini ili na kraju broja, nazivaju se značajnim. Broj 2330 ima 4 značajne znamenke, ali broj 6,1×10 2 ima samo dvije, a broj 0,0503 ima tri, budući da su nule lijevo od 5 beznačajne. Zapisivanje broja 2,39 znači da su sve decimale točne, a zapisivanje 1,2800 znači da su i treća i četvrta decimala točne. Broj 1,90 ima tri značajne znamenke i to znači da smo prilikom mjerenja uzeli u obzir ne samo jedinice, već i desetinke i stotinke, a broj 1,9 ima samo dvije značajne znamenke i to znači da smo uzeli u obzir cijelinu i desetinke i preciznost ove broj je 10 puta manji.

Pravila zaokruživanja brojeva

Prilikom zaokruživanja zadržavaju se samo ispravni znakovi, ostali se odbacuju.

1. Zaokruživanje se postiže jednostavnim odbacivanjem znamenki ako je prva od odbačenih znamenki manja od 5.

2. Ako je prva od odbačenih znamenki veća od 5, tada se zadnja znamenka povećava za jedan. Posljednja znamenka se također povećava kada je prva znamenka koja se odbacuje 5, nakon koje slijedi jedna ili više znamenki koje nisu nula.

Na primjer, različita zaokruživanja od 35,856 bila bi: 35,9; 36.

3. Ako je odbačena znamenka 5, a iza nje nema značajnih znamenki, tada se zaokružuje na najbliži paran broj, odnosno zadnja zadržana znamenka ostaje nepromijenjena ako je parna, a povećava se za jedan ako je neparna .

Na primjer, 0,435 zaokružuje se na 0,44; Zaokružujemo 0,365 na 0,36.

U ovoj ću temi napisati nešto poput kratke varalice o pogreškama. Opet, ovaj tekst nije ni na koji način služben i pozivanje na njega je neprihvatljivo. Bio bih zahvalan za ispravak svih grešaka ili netočnosti koje mogu biti u ovom tekstu.

Što je greška?

Zapisivanje rezultata pokusa oblika () znači da ako provedemo puno identičnih pokusa, tada će u 70% dobiveni rezultati ležati u intervalu, a u 30% neće.

Ili, što je isto, ako ponovimo eksperiment, tada će novi rezultat pasti unutar intervala pouzdanosti s vjerojatnošću jednakom vjerojatnosti povjerenja.

Kako zaokružiti grešku i rezultat?

Greška je zaokružena do prve značajne znamenke, ako nije jedan. Ako jedan - onda do dva. pri čemu značajna brojka poziva se bilo koja znamenka rezultata osim vodećih nula.

Zaokruži na ili ili ali ni u kom slučaju ili , budući da postoje 2 značajne brojke - 2 i 0 iza dvije.

Zaokružite na ili

Zaokružite na ili ili

Rezultat zaokružujemo tako da zadnja značajna znamenka rezultata odgovara zadnjoj značajnoj znamenki pogreške.

Primjeri ispravan unos:

mm

Hm, zadržimo pogrešku ovdje na 2 značajne znamenke jer je prva značajna brojka u pogrešci jedan.

mm

Primjeri netočan unos:

Mm. Ovdje dodatni znak kao rezultat. mm bit će točno.

mm. Ovdje dodatni znak i u pogrešci i kao rezultat. mm bit će točno.

U svom radu koristim vrijednost koja mi je dana jednostavno kao broj. Na primjer, masa utega. Koja mu je granica pogreške?

Ako greška nije izričito naznačena, možete uzeti jednu u zadnjoj znamenki. Odnosno, ako je napisano m = 1,35 g, tada grešku treba uzeti kao 0,01 g.

Postoji funkcija više veličina.Svaka od tih veličina ima svoju pogrešku. Da biste pronašli grešku funkcije, morate učiniti sljedeće:

Simbol označava parcijalnu derivaciju f u odnosu na x. Pročitajte više o parcijalnim izvedenicama.

Pretpostavimo da ste izmjerili istu količinu x nekoliko (n) puta. Dobili smo skup vrijednosti. . Morate izračunati pogrešku raspršenja, izračunati pogrešku instrumenta i zbrojiti ih.

Bodovi.

1. Izračunavamo pogrešku širenja

Ako se sve vrijednosti poklapaju, nemate širenja. U suprotnom, postoji pogreška raspršenja koju treba izračunati. Za početak, izračunava se korijen srednje kvadratne pogreške prosjeka:

Ovdje znači prosjek u odnosu na sve.
Pogreška raspršenja dobiva se množenjem srednje kvadratne pogreške srednje vrijednosti sa Studentovim koeficijentom, koji ovisi o vjerojatnosti pouzdanosti koju odaberete i broju mjerenja n:

Studentove koeficijente uzimamo iz donje tablice. Vjerojatnost pouzdanosti generira se proizvoljno, brojem mjerenja n također znamo.

2. Pogrešku instrumenta smatramo prosjekom

Ako su pogreške različitih točaka različite, onda prema formuli

Naravno, svačija vjerojatnost povjerenja trebala bi biti ista.

3. Dodajte prosjek s namazom

Pogreške se uvijek zbrajaju kao korijen kvadrata:

U ovom slučaju, morate biti sigurni da se vjerojatnosti pouzdanosti s kojima su izračunate i podudaraju.

Kako odrediti pogrešku instrumenta prosjeka iz grafikona? Pa, to jest, koristeći metodu uparenih točaka ili metodu najmanjih kvadrata, pronaći ćemo pogrešku u širenju prosječnog otpora. Kako pronaći pogrešku instrumenta prosječnog otpora?

I metoda najmanjih kvadrata i metoda uparenih točaka mogu dati točan odgovor na ovo pitanje. Za forum najmanjih kvadrata u Svetozarovu postoji ("Osnove...", odjeljak o metodi najmanjih kvadrata), a za uparene točke prvo što pada na pamet (u čelo, što se kaže) je izračunati instrumental greška svakog kutnog koeficijenta. Pa dalje po svim točkama...

Ako ne želite patiti, onda u laboratorijskim knjigama postoji jednostavan način procjene pogreška instrumenta kutnog koeficijenta, odnosno iz sljedećeg MNC-a (npr. prije rada 1 u laboratorijskoj knjizi "Električni mjerni instrumenti...." zadnja stranica Metodoloških preporuka).

Gdje je vrijednost najvećeg odstupanja duž osi Y točke s pogreškom od nacrtane ravne linije, a nazivnik je širina područja našeg grafikona duž osi Y. Isto tako i za os X.

Klasa točnosti ispisana je na spremniku otpora: 0,05/4*10^-6? Kako iz ovoga pronaći grešku instrumenta?

To znači da najveća relativna pogreška uređaja (u postocima) ima oblik:
, Gdje
- najveću vrijednost otpora spremnika i - nazivnu vrijednost uključenog otpora.
Lako je vidjeti da je drugi član važan kada radimo na vrlo niskim otporima.

Više detalja uvijek možete pronaći u putovnici uređaja. Putovnicu možete pronaći na internetu tako da u Google upišete marku uređaja.

Literatura o pogreškama

Puno više informacija o ovoj temi možete pronaći u knjizi preporučenoj brucošima:
V.V. Svetozarov "Elementarna obrada rezultata mjerenja"

Kao dodatnu (za brucoše dodatnu) literaturu možemo preporučiti:
V.V. Svetozarov "Osnove statističke obrade rezultata mjerenja"

A tko želi konačno sve shvatiti neka pogleda ovdje:
J. Taylor. "Uvod u teoriju pogrešaka"

Hvala vam što ste pronašli i objavili ove prekrasne knjige na svojoj stranici.