Să presupunem că Ahile aleargă de zece ori mai repede decât țestoasa și este la o mie de pași în spatele ei. În timpul necesar lui Ahile pentru a parcurge această distanță, țestoasa se va târa o sută de pași în aceeași direcție. Când Ahile aleargă o sută de pași, țestoasa se târăște încă zece pași și așa mai departe. Procesul va continua la infinit, Ahile nu va ajunge niciodată din urmă cu țestoasa.
Acest raționament a devenit un șoc logic pentru toate generațiile următoare. Aristotel, Diogene, Kant, Hegel, Hilbert... Toți au considerat într-un fel sau altul aporia lui Zenon. Șocul a fost atât de puternic încât " ... discuțiile continuă până în prezent comunitatea științifică nu a reușit încă să ajungă la o opinie comună asupra esenței paradoxurilor ... analiza matematică, teoria seturilor, noi abordări fizice și filozofice au fost implicate în studiul problemei; ; niciunul dintre ele nu a devenit o soluție general acceptată la problemă...„[Wikipedia, „Aporia lui Zeno”. Toată lumea înțelege că sunt păcăliți, dar nimeni nu înțelege în ce constă înșelăciunea.
Din punct de vedere matematic, Zenon în aporia sa a demonstrat clar trecerea de la cantitate la . Această tranziție presupune aplicare în loc de cele permanente. Din câte am înțeles, aparatul matematic pentru utilizarea unităților de măsură variabile fie nu a fost încă dezvoltat, fie nu a fost aplicat la aporia lui Zeno. Aplicarea logicii noastre obișnuite ne duce într-o capcană. Noi, datorită inerției gândirii, aplicăm unități constante de timp valorii reciproce. Din punct de vedere fizic, se pare că timpul încetinește până când se oprește complet în momentul în care Ahile ajunge din urmă cu țestoasa. Dacă timpul se oprește, Ahile nu mai poate depăși țestoasa.
Dacă ne întoarcem logica obișnuită, totul cade la locul său. Ahile aleargă cu o viteză constantă. Fiecare segment ulterior al drumului său este de zece ori mai scurt decât cel anterior. În consecință, timpul petrecut pentru depășirea acestuia este de zece ori mai mic decât cel anterior. Dacă aplicăm conceptul de „infinit” în această situație, atunci ar fi corect să spunem „Achile va ajunge din urmă broasca țestoasă infinit de repede”.
Cum să eviți această capcană logică? Rămâneți în unități constante de timp și nu treceți la unități reciproce. În limbajul lui Zeno arată astfel:
În timpul necesar lui Ahile să alerge o mie de pași, țestoasa se va târa o sută de pași în aceeași direcție. În următorul interval de timp egal cu primul, Ahile va alerga încă o mie de pași, iar țestoasa se va târa o sută de pași. Acum Ahile este cu opt sute de pași înaintea țestoasei.
Această abordare descrie în mod adecvat realitatea fără niciun paradox logic. Dar aceasta nu este o soluție completă a problemei. Afirmația lui Einstein despre irezistibilitatea vitezei luminii este foarte asemănătoare cu aporia lui Zeno „Achile și broasca țestoasă”. Mai trebuie să studiem, să regândim și să rezolvăm această problemă. Iar soluția trebuie căutată nu în număr infinit de mare, ci în unități de măsură.
O altă aporie interesantă a lui Zeno spune despre o săgeată zburătoare:
O săgeată zburătoare este nemișcată, deoarece în fiecare moment de timp este în repaus și, deoarece este în repaus în fiecare moment de timp, este întotdeauna în repaus.
În această aporie, paradoxul logic este depășit foarte simplu - este suficient să clarificăm că în fiecare moment de timp o săgeată zburătoare este în repaus în diferite puncte din spațiu, care, de fapt, este mișcare. Un alt punct trebuie remarcat aici. Dintr-o fotografie a unei mașini de pe șosea este imposibil să se determine nici faptul mișcării acesteia, fie distanța până la ea. Pentru a determina dacă o mașină se mișcă, aveți nevoie de două fotografii făcute din același punct în momente diferite, dar nu puteți determina distanța față de ele. Pentru a determina distanța până la o mașină, aveți nevoie de două fotografii făcute din diferite puncte ale spațiului la un moment dat, dar din ele nu puteți determina faptul de mișcare (desigur, mai aveți nevoie de date suplimentare pentru calcule, trigonometria vă va ajuta ). Ceea ce vreau să atrag atenția în mod deosebit este că două puncte în timp și două puncte în spațiu sunt lucruri diferite care nu trebuie confundate, deoarece oferă oportunități diferite de cercetare.
miercuri, 4 iulie 2018
Diferențele dintre set și multiset sunt descrise foarte bine pe Wikipedia. Să vedem.
După cum puteți vedea, „nu pot exista două elemente identice într-o mulțime”, dar dacă există elemente identice într-o mulțime, un astfel de set se numește „multiset”. Ființele rezonabile nu vor înțelege niciodată o asemenea logică absurdă. Acesta este nivelul papagalilor vorbitori și al maimuțelor dresate, care nu au inteligență din cuvântul „complet”. Matematicienii acționează ca formatori obișnuiți, propovăduindu-ne ideile lor absurde.
Pe vremuri, inginerii care au construit podul se aflau într-o barcă sub pod în timp ce testau podul. Dacă podul s-a prăbușit, inginerul mediocru a murit sub dărâmăturile creației sale. Dacă podul putea rezista la sarcină, talentatul inginer a construit alte poduri.
Indiferent de cât de matematicieni se ascund în spatele expresiei „amintește-mă, sunt în casă” sau, mai degrabă, „matematica studiază concepte abstracte”, există un cordon ombilical care le conectează inextricabil cu realitatea. Acest cordon ombilical este bani. Să aplicăm teoria mulțimilor matematicienilor înșiși.
Am studiat foarte bine matematica și acum stăm la casa de marcat, dăm salarii. Deci un matematician vine la noi pentru banii lui. Îi numărăm întreaga sumă și o așezăm pe masa noastră în grămezi diferite, în care punem bancnote de aceeași valoare. Apoi luăm o bancnotă din fiecare grămadă și îi dăm matematicianului „setul său matematic de salariu”. Să-i explicăm matematicianului că va primi bancnotele rămase doar atunci când va dovedi că o mulțime fără elemente identice nu este egală cu o mulțime cu elemente identice. Aici începe distracția.
În primul rând, logica deputaților va funcționa: „Acest lucru se poate aplica și altora, dar nu și mie!” Apoi vor începe să ne liniștească că bancnotele de aceeași denominație au numere de bancnote diferite, ceea ce înseamnă că nu pot fi considerate aceleași elemente. Bine, să numărăm salariile în monede - nu există numere pe monede. Aici matematicianul va începe să-și amintească frenetic de fizică: diferite monede au cantități diferite de murdărie, structura cristalină și aranjarea atomilor este unică pentru fiecare monedă...
Și acum am cea mai interesantă întrebare: unde este linia dincolo de care elementele unui multiset se transformă în elemente ale unui set și invers? O astfel de linie nu există - totul este hotărât de șamani, știința nu este nici măcar aproape să zacă aici.
Uite aici. Selectăm stadioane de fotbal cu aceeași suprafață de teren. Zonele câmpurilor sunt aceleași - ceea ce înseamnă că avem un multiset. Dar dacă ne uităm la numele acestor stadioane, obținem multe, pentru că numele sunt diferite. După cum puteți vedea, același set de elemente este atât un set, cât și un multiset. Care este corect? Și aici matematicianul-șamanul-ascuțitor scoate un as de atuuri din mânecă și începe să ne vorbească fie despre un set, fie despre un multiset. În orice caz, ne va convinge că are dreptate.
Pentru a înțelege cum funcționează șamanii moderni cu teoria mulțimilor, legând-o de realitate, este suficient să răspundem la o întrebare: prin ce diferă elementele unui set de elementele altui set? Vă voi arăta, fără niciun „conceput ca nu un singur întreg” sau „neconceput ca un singur întreg”.
Duminică, 18 martie 2018
Suma cifrelor unui număr este un dans al șamanilor cu o tamburină, care nu are nimic de-a face cu matematica. Da, la lecțiile de matematică suntem învățați să găsim suma cifrelor unui număr și să o folosim, dar de aceea ei sunt șamani, pentru a-și învăța descendenții abilitățile și înțelepciunea, altfel șamanii pur și simplu vor muri.
Ai nevoie de dovezi? Deschideți Wikipedia și încercați să găsiți pagina „Suma cifrelor unui număr”. Ea nu există. Nu există nicio formulă în matematică care să poată fi folosită pentru a găsi suma cifrelor oricărui număr. La urma urmei, numerele sunt simboluri grafice cu care scriem numere, iar în limbajul matematicii sarcina sună astfel: „Găsiți suma simbolurilor grafice care reprezintă orice număr”. Matematicienii nu pot rezolva această problemă, dar șamanii o pot face cu ușurință.
Să ne dăm seama ce și cum facem pentru a găsi suma cifrelor unui număr dat. Și așa, să avem numărul 12345. Ce trebuie făcut pentru a găsi suma cifrelor acestui număr? Să luăm în considerare toți pașii în ordine.
1. Notează numărul pe o foaie de hârtie. Ce am făcut? Am convertit numărul într-un simbol numeric grafic. Aceasta nu este o operație matematică.
2. Tăiem o imagine rezultată în mai multe imagini care conțin numere individuale. Decuparea unei imagini nu este o operație matematică.
3. Convertiți simbolurile grafice individuale în numere. Aceasta nu este o operație matematică.
4. Adăugați numerele rezultate. Acum asta e matematica.
Suma cifrelor numărului 12345 este 15. Acestea sunt „cursurile de tăiere și cusut” predate de șamani pe care le folosesc matematicienii. Dar asta nu este tot.
Din punct de vedere matematic, nu contează în ce sistem de numere scriem un număr. Deci, în sisteme de numere diferite, suma cifrelor aceluiași număr va fi diferită. În matematică, sistemul numeric este indicat ca indice în dreapta numărului. Cu numărul mare 12345, nu vreau să-mi păcălesc capul, să luăm în considerare numărul 26 din articolul despre. Să scriem acest număr în sisteme de numere binar, octal, zecimal și hexazecimal. Nu ne vom uita la fiecare pas la microscop, am făcut-o deja. Să ne uităm la rezultat.
După cum puteți vedea, în sisteme numerice diferite, suma cifrelor aceluiași număr este diferită. Acest rezultat nu are nimic de-a face cu matematica. Este la fel ca și cum ai determina aria unui dreptunghi în metri și centimetri, ai obține rezultate complet diferite.
Zero arată la fel în toate sistemele de numere și nu are sumă de cifre. Acesta este un alt argument în favoarea faptului că. Întrebare pentru matematicieni: cum este ceva care nu este un număr desemnat în matematică? Ce, pentru matematicieni nu există nimic în afară de numere? Pot permite asta șamanilor, dar nu și oamenilor de știință. Realitatea nu este doar despre cifre.
Rezultatul obținut ar trebui considerat ca o dovadă că sistemele numerice sunt unități de măsură pentru numere. La urma urmei, nu putem compara numerele cu unități de măsură diferite. Dacă aceleași acțiuni cu diferite unități de măsură ale aceleiași mărimi duc la rezultate diferite după compararea lor, atunci acest lucru nu are nimic de-a face cu matematica.
Ce este matematica reală? Acesta este momentul în care rezultatul unei operații matematice nu depinde de mărimea numărului, de unitatea de măsură folosită și de cine efectuează această acțiune.
Oh! Asta nu este toaleta pentru femei?
-Tânără! Acesta este un laborator pentru studiul sfințeniei nefilice a sufletelor în timpul înălțării lor la cer! Halo în partea de sus și săgeată în sus. Ce altă toaletă?
Femeie... Aureola de sus și săgeata în jos sunt masculine.
Dacă o astfel de operă de artă de design îți fulgerează în fața ochilor de mai multe ori pe zi,
Atunci nu este surprinzător că găsiți brusc o pictogramă ciudată în mașina dvs.:
Personal, fac un efort să văd minus patru grade la o persoană care face caca (o poză) (o compoziție din mai multe imagini: semnul minus, numărul patru, desemnarea gradului). Și nu cred că această fată este o proastă care nu știe fizică. Ea are doar un stereotip puternic de a percepe imaginile grafice. Și matematicienii ne învață asta tot timpul. Iată un exemplu.
1A nu este „minus patru grade” sau „unu a”. Acesta este „pooping om” sau numărul „douăzeci și șase” în notație hexazecimală. Acei oameni care lucrează constant în acest sistem numeric percep automat un număr și o literă ca un simbol grafic.
La cursurile de gimnaziu și liceu, elevii au abordat tema „Fracțiuni”. Cu toate acestea, acest concept este mult mai larg decât ceea ce este dat în procesul de învățare. Astăzi, conceptul de fracție este întâlnit destul de des și nu toată lumea poate calcula orice expresie, de exemplu, înmulțirea fracțiilor.
Ce este o fracție?
Din punct de vedere istoric, numerele fracționale au apărut din necesitatea de a măsura. După cum arată practica, există adesea exemple de determinare a lungimii unui segment și a volumului unui dreptunghi dreptunghiular.
Inițial, elevii sunt introduși în conceptul de acțiune. De exemplu, dacă împărțiți un pepene verde în 8 părți, atunci fiecare persoană va primi o opteme din pepene. Această parte din opt se numește cotă.
O cotă egală cu ½ din orice valoare se numește jumătate; ⅓ - a treia; ¼ - un sfert. Înregistrările de forma 5/8, 4/5, 2/4 se numesc fracții ordinare. O fracție comună este împărțită în numărător și numitor. Între ele se află bara de fracțiuni sau bara de fracțiuni. Linia fracțională poate fi trasată fie ca o linie orizontală, fie ca o linie oblică. În acest caz, denotă semnul diviziunii.

Numitorul reprezintă în câte părți egale este împărțită cantitatea sau obiectul; iar numărătorul este câte acțiuni identice sunt luate. Numătorul este scris deasupra liniei fracțiilor, numitorul este scris sub ea.
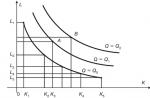
Cel mai convenabil este să afișați fracțiile obișnuite pe o rază de coordonate. Dacă un singur segment este împărțit în 4 părți egale, fiecare parte este desemnată printr-o literă latină, atunci rezultatul poate fi un ajutor vizual excelent. Deci, punctul A arată o cotă egală cu 1/4 din întregul segment de unitate, iar punctul B marchează 2/8 dintr-un segment dat.

Tipuri de fracții
Fracțiile pot fi numere ordinare, zecimale și mixte. În plus, fracțiile pot fi împărțite în adecvate și improprii. Această clasificare este mai potrivită pentru fracțiile obișnuite.
O fracție proprie este un număr al cărui numărător este mai mic decât numitorul său. În consecință, o fracție improprie este un număr al cărui numărător este mai mare decât numitorul său. Al doilea tip este de obicei scris ca un număr mixt. Această expresie constă dintr-un număr întreg și o parte fracțională. De exemplu, 1½. 1 este o parte întreagă, ½ este o parte fracțională. Cu toate acestea, dacă trebuie să efectuați unele manipulări cu expresia (împărțirea sau înmulțirea fracțiilor, reducerea sau conversia acestora), numărul mixt este convertit într-o fracție improprie.
O expresie fracțională corectă este întotdeauna mai mică decât unu, iar una incorectă este întotdeauna mai mare sau egală cu 1.
În ceea ce privește această expresie, înțelegem o înregistrare în care este reprezentat orice număr, al cărui numitor al expresiei fracționale poate fi exprimat în termeni de unul cu mai multe zerouri. Dacă fracția este corectă, atunci partea întreagă în notație zecimală va fi egală cu zero.
Pentru a scrie o fracție zecimală, trebuie mai întâi să scrieți întreaga parte, să o separați de fracție folosind o virgulă și apoi să scrieți expresia fracției. Trebuie reținut că după virgulă zecimală numărătorul trebuie să conțină același număr de caractere digitale ca și zerouri în numitor.
Exemplu. Exprimați fracția 7 21 / 1000 în notație zecimală.

Algoritm pentru conversia unei fracții improprie într-un număr mixt și invers
Este incorect să scrieți o fracție necorespunzătoare în răspunsul la o problemă, așa că trebuie convertită într-un număr mixt:
- împărțiți numărătorul la numitorul existent;
- într-un exemplu specific, un coeficient incomplet este un întreg;
- iar restul este numărătorul părții fracționale, numitorul rămânând neschimbat.
Exemplu. Transformă fracția improprie în număr mixt: 47 / 5.
Soluţie. 47: 5. Coeficientul parțial este 9, restul = 2. Deci, 47 / 5 = 9 2 / 5.
Uneori trebuie să reprezentați un număr mixt ca o fracție improprie. Apoi, trebuie să utilizați următorul algoritm:
- partea întreagă se înmulțește cu numitorul expresiei fracționale;
- produsul rezultat se adaugă la numărător;
- rezultatul se scrie la numărător, numitorul rămâne neschimbat.
Exemplu. Prezintă numărul în formă mixtă ca o fracție improprie: 9 8 / 10.
Soluţie. 9 x 10 + 8 = 90 + 8 = 98 este numărătorul.
Răspuns: 98 / 10.
Înmulțirea fracțiilor
Pe fracții obișnuite pot fi efectuate diverse operații algebrice. Pentru a înmulți două numere, trebuie să înmulțiți numărătorul cu numărătorul și numitorul cu numitorul. În plus, înmulțirea fracțiilor cu numitori diferiți nu este diferită de înmulțirea fracțiilor cu aceiași numitori.

Se întâmplă că, după găsirea rezultatului, trebuie să reduceți fracția. Este imperativ să simplificați cât mai mult posibil expresia rezultată. Desigur, nu se poate spune că o fracție improprie dintr-un răspuns este o eroare, dar este și dificil să o numim răspuns corect.
Exemplu. Aflați produsul a două fracții ordinare: ½ și 20/18.

După cum se poate observa din exemplu, după găsirea produsului, se obține o notație fracțională reductibilă. Atât numărătorul, cât și numitorul în acest caz sunt împărțiți la 4, iar rezultatul este răspunsul 5 / 9.
Înmulțirea fracțiilor zecimale
Produsul fracțiilor zecimale este destul de diferit de produsul fracțiilor obișnuite în principiu. Deci, înmulțirea fracțiilor este după cum urmează:
- două fracții zecimale trebuie să fie scrise una sub cealaltă, astfel încât cifrele din dreapta să fie una sub cealaltă;
- trebuie să înmulțiți numerele scrise, în ciuda virgulelor, adică ca numere naturale;
- numărați numărul de cifre după punctul zecimal din fiecare număr;
- în rezultatul obținut după înmulțire, trebuie să numărați de la dreapta câte simboluri digitale sunt conținute în suma în ambii factori după virgulă zecimală și să puneți un semn de separare;
- dacă există mai puține numere în produs, atunci trebuie să scrieți cât mai multe zerouri în fața lor pentru a acoperi acest număr, puneți o virgulă și adăugați întreaga parte egală cu zero.

Exemplu. Calculați produsul a două fracții zecimale: 2,25 și 3,6.
Soluţie.

Înmulțirea fracțiilor mixte
Pentru a calcula produsul a două fracții mixte, trebuie să utilizați regula pentru înmulțirea fracțiilor:
- converti numere mixte în fracții improprii;
- găsiți produsul numărătorilor;
- găsiți produsul numitorilor;
- notează rezultatul;
- simplifica pe cât posibil expresia.
Exemplu. Aflați produsul dintre 4½ și 6 2/5.

Înmulțirea unui număr cu o fracție (fracții cu un număr)
Pe lângă găsirea produsului a două fracții și a numerelor mixte, există sarcini în care trebuie să înmulțiți cu o fracție.
Deci, pentru a găsi produsul dintre o fracție zecimală și un număr natural, aveți nevoie de:
- scrieți numărul sub fracție, astfel încât cifrele din dreapta să fie una deasupra celeilalte;
- găsiți produsul în ciuda virgulei;
- în rezultatul rezultat, separă partea întreagă de partea fracțională folosind o virgulă, numărând din dreapta numărul de cifre care se află după virgulă zecimală în fracție.
Pentru a înmulți o fracție comună cu un număr, trebuie să găsiți produsul dintre numărător și factorul natural. Dacă răspunsul produce o fracție care poate fi redusă, aceasta ar trebui convertită.
Exemplu. Calculați produsul dintre 5 / 8 și 12.
Soluţie. 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Răspuns: 7 1 / 2.
După cum puteți vedea din exemplul anterior, a fost necesar să reduceți rezultatul rezultat și să convertiți expresia fracțională incorectă într-un număr mixt.
Înmulțirea fracțiilor se referă și la găsirea produsului unui număr în formă mixtă și a unui factor natural. Pentru a înmulți aceste două numere, ar trebui să înmulțiți întreaga parte a factorului mixt cu număr, să înmulțiți numărătorul cu aceeași valoare și să lăsați numitorul neschimbat. Dacă este necesar, trebuie să simplificați rezultatul rezultat cât mai mult posibil.
Exemplu. Aflați produsul lui 9 5 / 6 și 9.
Soluţie. 9 5 / 6 x 9 = 9 x 9 + (5 x 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Răspuns: 88 1 / 2.
Înmulțirea cu factori de 10, 100, 1000 sau 0,1; 0,01; 0,001
Din paragraful precedent rezultă următoarea regulă. Pentru a înmulți o fracție zecimală cu 10, 100, 1000, 10000 etc., trebuie să mutați punctul zecimal la dreapta cu atâtea cifre câte zerouri există în factorul după unu.
Exemplul 1. Aflați produsul dintre 0,065 și 1000.
Soluţie. 0,065 x 1000 = 0065 = 65.
Răspuns: 65.
Exemplul 2. Aflați produsul dintre 3,9 și 1000.
Soluţie. 3,9 x 1000 = 3,900 x 1000 = 3900.
Răspuns: 3900.
Dacă trebuie să înmulțiți un număr natural și 0,1; 0,01; 0,001; 0,0001 etc., ar trebui să mutați virgula din produsul rezultat la stânga cu atâtea caractere cifre câte zerouri sunt înaintea unu. Dacă este necesar, înaintea numărului natural sunt scrise un număr suficient de zerouri.
Exemplul 1. Aflați produsul dintre 56 și 0,01.
Soluţie. 56 x 0,01 = 0056 = 0,56.
Răspuns: 0,56.
Exemplul 2. Aflați produsul dintre 4 și 0,001.
Soluţie. 4 x 0,001 = 0004 = 0,004.
Răspuns: 0,004.
Deci, găsirea produsului diferitelor fracții nu ar trebui să provoace dificultăți, cu excepția poate calcula rezultatul; în acest caz, pur și simplu nu puteți face fără un calculator.
Vom lua în considerare înmulțirea fracțiilor obișnuite în mai multe opțiuni posibile.
Înmulțirea unei fracții comune cu o fracție
Acesta este cel mai simplu caz în care trebuie să utilizați următoarele reguli de înmulțire a fracțiilor.
La înmulțiți fracția cu fracția, necesar:
- înmulțiți numărătorul primei fracții cu numărătorul celei de-a doua fracții și scrieți produsul lor în numărătorul noii fracții;
- înmulțiți numitorul primei fracții cu numitorul celei de-a doua fracții și scrieți produsul lor în numitorul noii fracții;
- Adunarea fracțiilor cu numitori similari
- Adunarea fracțiilor cu numitori diferiți
Înainte de a înmulți numărătorii și numitorii, verificați dacă fracțiile pot fi reduse. Reducerea fracțiilor în calcule vă va ușura mult calculele.

Înmulțirea unei fracții cu un număr natural
A face o fracție înmulțiți cu un număr natural Trebuie să înmulțiți numărătorul fracției cu acest număr și să lăsați numitorul fracției neschimbat.
Dacă rezultatul înmulțirii este o fracție necorespunzătoare, nu uitați să o transformați într-un număr mixt, adică evidențiați întreaga parte.

Înmulțirea numerelor mixte
Pentru a înmulți numere mixte, trebuie mai întâi să le transformați în fracții improprii și apoi să înmulțiți conform regulii de înmulțire a fracțiilor obișnuite.

O altă modalitate de a înmulți o fracție cu un număr natural
Uneori, atunci când faceți calcule, este mai convenabil să folosiți o altă metodă de înmulțire a unei fracții comune cu un număr.
Pentru a înmulți o fracție cu un număr natural, trebuie să împărțiți numitorul fracției la acest număr și să lăsați numărătorul același.

După cum se poate vedea din exemplu, această versiune a regulii este mai convenabilă de utilizat dacă numitorul fracției este divizibil cu un număr natural fără rest.
Operații cu fracții
Adunarea fracțiilor cu numitori similari
Există două tipuri de adunări de fracții:
Mai întâi, să învățăm adunarea fracțiilor cu numitori similari. Totul este simplu aici. Pentru a adăuga fracții cu aceiași numitori, trebuie să adăugați numărătorii lor și să lăsați numitorul neschimbat. De exemplu, să adăugăm fracțiile și . Adăugați numărătorii și lăsați numitorul neschimbat:

Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în patru părți. Dacă adăugați pizza la pizza, obțineți pizza:
Exemplul 2. Adăugați fracții și .
Din nou, adunăm numărătorii și lăsăm numitorul neschimbat:

Răspunsul s-a dovedit a fi o fracție improprie. Când vine sfârșitul sarcinii, se obișnuiește să scapi de fracțiile improprii. Pentru a scăpa de o fracție necorespunzătoare, trebuie să selectați întreaga parte a acesteia. În cazul nostru, întreaga parte este ușor de izolat - doi împărțiți la doi egal cu unul:

Acest exemplu poate fi ușor de înțeles dacă ne amintim despre o pizza care este împărțită în două părți. Dacă adăugați mai multă pizza la pizza, obțineți o pizza întreagă:
Exemplul 3. Adăugați fracții și .
![]()
Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în trei părți. Dacă adăugați mai multă pizza la pizza, obțineți pizza:
Exemplul 4. Găsiți valoarea unei expresii 
Acest exemplu este rezolvat exact în același mod ca și cele precedente. Număratorii trebuie adăugați și numitorul lăsat neschimbat:
Să încercăm să descriem soluția noastră folosind un desen. Dacă adăugați pizza la o pizza și adăugați mai multe pizza, obțineți 1 pizza întreagă și mai multe pizza.
După cum puteți vedea, nu este nimic complicat în adunarea fracțiilor cu aceiași numitori. Este suficient să înțelegeți următoarele reguli:
- Pentru a adăuga fracții cu același numitor, trebuie să adăugați numărătorii lor și să lăsați numitorul același;
- Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, atunci trebuie să evidențiați întreaga parte a acestuia.
- Aflați LCM al numitorilor fracțiilor;
- Împărțiți LCM la numitorul fiecărei fracții și obțineți un factor suplimentar pentru fiecare fracție;
- Înmulțiți numărătorii și numitorii fracțiilor cu factorii suplimentari ai acestora;
- Adaugă fracții care au aceiași numitori;
- Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, atunci selectați întreaga sa parte;
- Scăderea fracțiilor cu numitori similari
- Scăderea fracțiilor cu numitori diferiți
Adunarea fracțiilor cu numitori diferiți
Acum să învățăm cum să adunăm fracții cu numitori diferiți. Când se adună fracții, numitorii fracțiilor trebuie să fie aceiași. Dar nu sunt întotdeauna la fel.
De exemplu, fracțiile pot fi adăugate deoarece au aceiași numitori.
Dar fracțiile nu pot fi adăugate imediat, deoarece aceste fracții au numitori diferiți. În astfel de cazuri, fracțiile trebuie reduse la același numitor (comun).
Există mai multe moduri de a reduce fracțiile la același numitor. Astăzi ne vom uita doar la una dintre ele, deoarece celelalte metode pot părea complicate pentru un începător.
Esența acestei metode este că mai întâi căutăm cel mai mic multiplu comun (LCM) al numitorilor ambelor fracții. LCM este apoi împărțit la numitorul primei fracții pentru a obține primul factor suplimentar. Ei fac același lucru cu a doua fracție - LCM este împărțit la numitorul celei de-a doua fracții și se obține un al doilea factor suplimentar.
Numătorii și numitorii fracțiilor sunt apoi înmulțiți cu factorii lor suplimentari. Ca urmare a acestor acțiuni, fracțiile care au numitori diferiți sunt convertite în fracții care au aceiași numitori. Și știm deja cum să adunăm astfel de fracții.
Exemplul 1. Să adăugăm fracțiile și
Aceste fracții au numitori diferiți, așa că trebuie să le reduceți la același numitor (comun).
În primul rând, găsim cel mai mic multiplu comun al numitorilor ambelor fracții. Numitorul primei fracții este numărul 3, iar numitorul celei de-a doua fracții este numărul 2. Cel mai mic multiplu comun al acestor numere este 6
LCM (2 și 3) = 6
Acum să revenim la fracții și . Mai întâi, împărțiți LCM la numitorul primei fracții și obțineți primul factor suplimentar. LCM este numărul 6, iar numitorul primei fracții este numărul 3. Împărțind 6 la 3, obținem 2.
Numărul rezultat 2 este primul multiplicator suplimentar. O notăm până la prima fracție. Pentru a face acest lucru, faceți o linie oblică mică peste fracție și notați factorul suplimentar găsit deasupra ei:
Facem același lucru cu a doua fracție. Împărțim LCM la numitorul celei de-a doua fracții și obținem al doilea factor suplimentar. LCM este numărul 6, iar numitorul celei de-a doua fracții este numărul 2. Împărțind 6 la 2, obținem 3.
Numărul 3 rezultat este al doilea multiplicator suplimentar. O scriem la a doua fracție. Din nou, facem o linie oblică mică peste a doua fracție și notăm factorul suplimentar găsit deasupra ei:
Acum avem totul pregătit pentru adăugare. Rămâne să înmulțiți numărătorii și numitorii fracțiilor cu factorii lor suplimentari:

Privește cu atenție la ce am ajuns. Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori. Și știm deja cum să adunăm astfel de fracții. Să luăm acest exemplu până la capăt:

Acest lucru completează exemplul. Se dovedește a adăuga.
Să încercăm să descriem soluția noastră folosind un desen. Dacă adăugați pizza la o pizza, obțineți o pizza întreagă și o altă șesime dintr-o pizza:
Reducerea fracțiilor la același numitor (comun) poate fi, de asemenea, descrisă folosind o imagine. Reducând fracțiile și la un numitor comun, am obținut fracțiile și . Aceste două fracții vor fi reprezentate de aceleași bucăți de pizza. Singura diferență va fi că de data aceasta vor fi împărțite în părți egale (reduse la același numitor).

Primul desen reprezintă o fracție (patru piese din șase), iar al doilea desen reprezintă o fracție (trei piese din șase). Adăugând aceste piese obținem (șapte bucăți din șase). Această fracție este improprie, așa că am evidențiat întreaga parte a ei. Drept urmare, am primit (o pizza întreagă și o altă pizza a șasea).
Vă rugăm să rețineți că am descris acest exemplu prea detaliat. În instituțiile de învățământ nu este obișnuit să scrieți atât de detaliat. Trebuie să puteți găsi rapid LCM-ul ambilor numitori și factori suplimentari la aceștia, precum și să înmulțiți rapid factorii suplimentari găsiți cu numărătorii și numitorii dvs. Dacă am fi la școală, ar trebui să scriem acest exemplu după cum urmează:

Dar există și o altă față a monedei. Dacă nu luați note detaliate în primele etape ale studiului matematicii, atunci încep să apară întrebări de acest fel. „De unde vine acel număr?”, „De ce fracțiile se transformă brusc în fracții complet diferite? «.
Pentru a facilita adăugarea fracțiilor cu numitori diferiți, puteți folosi următoarele instrucțiuni pas cu pas:
Exemplul 2. Găsiți valoarea unei expresii  .
.
Să folosim diagrama oferită mai sus.
Pasul 1. Găsiți LCM pentru numitorii fracțiilor
Găsiți LCM pentru numitorii ambelor fracții. Numitorii fracțiilor sunt numerele 2, 3 și 4. Trebuie să găsiți LCM pentru aceste numere:
Pasul 2. Împărțiți LCM la numitorul fiecărei fracții și obțineți un factor suplimentar pentru fiecare fracție
Împărțiți LCM la numitorul primei fracții. LCM este numărul 12, iar numitorul primei fracții este numărul 2. Împărțim 12 la 2, obținem 6. Primul factor suplimentar este 6. Îl scriem deasupra primei fracții:
Acum împărțim LCM la numitorul celei de-a doua fracții. LCM este numărul 12, iar numitorul celei de-a doua fracții este numărul 3. Împărțim 12 la 3, obținem 4. Obținem al doilea factor suplimentar 4. Îl scriem deasupra celei de-a doua fracții:
Acum împărțim LCM la numitorul celei de-a treia fracții. LCM este numărul 12, iar numitorul celei de-a treia fracții este numărul 4. Împărțim 12 la 4, obținem 3. Obținem al treilea factor suplimentar 3. Îl scriem deasupra celei de-a treia fracții:
Pasul 3. Înmulțiți numărătorii și numitorii fracțiilor cu factorii suplimentari ai acestora
Înmulțim numărătorii și numitorii cu factorii lor suplimentari:
Pasul 4. Adaugă fracții cu aceiași numitori
Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori (comuni). Tot ce rămâne este să adunăm aceste fracții. Adaugă:

Adăugarea nu se potrivea pe o singură linie, așa că am mutat expresia rămasă pe următoarea linie. Acest lucru este permis la matematică. Când o expresie nu se încadrează pe o linie, este mutată pe următoarea linie și este necesar să se pună un semn egal (=) la sfârșitul primei rânduri și la începutul noii linii. Semnul egal de pe a doua linie indică faptul că aceasta este o continuare a expresiei care a fost pe prima linie.
Pasul 5. Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, atunci evidențiați întreaga sa parte
Răspunsul nostru s-a dovedit a fi o fracție improprie. Trebuie să evidențiem o întreagă parte din ea. Subliniem:

Am primit un răspuns
Scăderea fracțiilor cu numitori similari
Există două tipuri de scădere de fracții:
În primul rând, să învățăm cum să scădem fracții cu numitori similari. Totul este simplu aici. Pentru a scădea altul dintr-o fracție, trebuie să scădeți numărătorul celei de-a doua fracții de la numărătorul primei fracții, dar numitorul rămâne același.
De exemplu, să găsim valoarea expresiei . Pentru a rezolva acest exemplu, trebuie să scădeți numărătorul celei de-a doua fracții din numărătorul primei fracții și să lăsați numitorul același. Să facem asta:

Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în patru părți. Dacă tăiați pizza dintr-o pizza, obțineți pizza:
Exemplul 2. Găsiți valoarea expresiei.
Din nou, de la numărătorul primei fracții, scădeți numărătorul celei de-a doua fracții și lăsați numitorul același:

Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în trei părți. Dacă tăiați pizza dintr-o pizza, obțineți pizza:
Exemplul 3. Găsiți valoarea unei expresii 
Acest exemplu este rezolvat exact în același mod ca și cele precedente. Din numărătorul primei fracții trebuie să scădeți numărătorii fracțiilor rămase:

Răspunsul a fost o fracție improprie. Dacă exemplul este completat, atunci se obișnuiește să scapi de fracția necorespunzătoare. Să scăpăm de fracția improprie din răspuns. Pentru a face acest lucru, să selectăm întreaga sa parte:
După cum puteți vedea, nu este nimic complicat în scăderea fracțiilor cu aceiași numitori. Este suficient să înțelegeți următoarele reguli:
Scăderea fracțiilor cu numitori diferiți
De exemplu, puteți scădea o fracție dintr-o fracție deoarece fracțiile au aceiași numitori. Dar nu puteți scădea o fracție dintr-o fracție, deoarece aceste fracții au numitori diferiți. În astfel de cazuri, fracțiile trebuie reduse la același numitor (comun).
Numitorul comun se găsește folosind același principiu pe care l-am folosit atunci când adunăm fracții cu numitori diferiți. În primul rând, găsiți LCM al numitorilor ambelor fracții. Apoi LCM se împarte la numitorul primei fracții și se obține primul factor suplimentar, care se scrie deasupra primei fracții. În mod similar, LCM este împărțit la numitorul celei de-a doua fracții și se obține un al doilea factor suplimentar, care este scris deasupra celei de-a doua fracții.
Fracțiile sunt apoi înmulțite cu factorii lor suplimentari. Ca rezultat al acestor operații, fracțiile care au numitori diferiți sunt convertite în fracții care au aceiași numitori. Și știm deja cum să scădem astfel de fracții.
Exemplul 1. Găsiți sensul expresiei:
Mai întâi găsim LCM al numitorilor ambelor fracții. Numitorul primei fracții este numărul 3, iar numitorul celei de-a doua fracții este numărul 4. Cel mai mic multiplu comun al acestor numere este 12
LCM (3 și 4) = 12
Acum să revenim la fracții și
Să găsim un factor suplimentar pentru prima fracție. Pentru a face acest lucru, împărțiți LCM la numitorul primei fracții. LCM este numărul 12, iar numitorul primei fracții este numărul 3. Împărțiți 12 la 3, obținem 4. Scrieți un patru deasupra primei fracții:
Facem același lucru cu a doua fracție. Împărțiți LCM la numitorul celei de-a doua fracții. LCM este numărul 12, iar numitorul celei de-a doua fracții este numărul 4. Împărțiți 12 la 4, obținem 3. Scrieți un trei peste a doua fracție:
Acum suntem pregătiți pentru scădere. Rămâne să înmulțim fracțiile cu factorii lor suplimentari:

Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori. Și știm deja cum să scădem astfel de fracții. Să luăm acest exemplu până la capăt:

Am primit un răspuns
Să încercăm să descriem soluția noastră folosind un desen. Dacă tăiați pizza dintr-o pizza, obțineți pizza
Aceasta este versiunea detaliată a soluției. Dacă am fi la școală, ar trebui să rezolvăm mai scurt acest exemplu. O astfel de soluție ar arăta astfel:

Reducerea fracțiilor la un numitor comun poate fi reprezentată și folosind o imagine. Reducând aceste fracții la un numitor comun, am obținut fracțiile și . Aceste fracții vor fi reprezentate de aceleași felii de pizza, dar de data aceasta vor fi împărțite în părți egale (reduse la același numitor):

Prima imagine arată o fracție (opt bucăți din douăsprezece), iar a doua imagine arată o fracție (trei bucăți din douăsprezece). Tăiind trei bucăți din opt bucăți, obținem cinci bucăți din douăsprezece. Fracția descrie aceste cinci piese.
Exemplul 2. Găsiți valoarea unei expresii 
Aceste fracții au numitori diferiți, așa că mai întâi trebuie să le reduceți la același numitor (comun).
Să găsim LCM al numitorilor acestor fracții.
Numitorii fracțiilor sunt numerele 10, 3 și 5. Cel mai mic multiplu comun al acestor numere este 30
LCM(10, 3, 5) = 30
Acum găsim factori suplimentari pentru fiecare fracție. Pentru a face acest lucru, împărțiți LCM la numitorul fiecărei fracții.
Să găsim un factor suplimentar pentru prima fracție. LCM este numărul 30, iar numitorul primei fracții este numărul 10. Împărțim 30 la 10, obținem primul factor suplimentar 3. Îl scriem deasupra primei fracții:
Acum găsim un factor suplimentar pentru a doua fracție. Împărțiți LCM la numitorul celei de-a doua fracții. LCM este numărul 30, iar numitorul celei de-a doua fracții este numărul 3. Împărțim 30 la 3, obținem al doilea factor suplimentar 10. Îl scriem deasupra celei de-a doua fracții:
Acum găsim un factor suplimentar pentru a treia fracție. Împărțiți LCM la numitorul celei de-a treia fracții. LCM este numărul 30, iar numitorul celei de-a treia fracții este numărul 5. Împărțim 30 la 5, obținem al treilea factor suplimentar 6. Îl scriem deasupra celei de-a treia fracții:
Acum totul este gata pentru scădere. Rămâne să înmulțim fracțiile cu factorii lor suplimentari:
Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori (comuni). Și știm deja cum să scădem astfel de fracții. Să terminăm acest exemplu.
Continuarea exemplului nu se va potrivi pe o linie, așa că mutam continuarea pe următoarea linie. Nu uitați de semnul egal (=) pe noua linie:

Răspunsul s-a dovedit a fi o fracțiune obișnuită și totul pare să ni se potrivească, dar este prea greoi și urât. Ar fi necesar să fie mai simplu și mai plăcut din punct de vedere estetic. Ce se poate face? Puteți scurta această fracție. Amintiți-vă că reducerea unei fracții este împărțirea numărătorului și numitorului cu cel mai mare divizor comun al numărătorului și numitorului.
Pentru a reduce corect o fracție, trebuie să împărțiți numărătorul și numitorul acesteia la cel mai mare divizor comun (MCD) al numerelor 20 și 30.
GCD nu trebuie confundat cu NOC. Cea mai frecventă greșeală a multor începători. GCD este cel mai mare divizor comun. Găsim că reduce o fracție.
Și LCM este cel mai mic multiplu comun. O găsim pentru a aduce fracții la același numitor (comun).
Acum vom găsi cel mai mare divizor comun (MCD) al numerelor 20 și 30.
Deci, găsim GCD pentru numerele 20 și 30:
GCD (20 și 30) = 10
Acum revenim la exemplul nostru și împărțim numărătorul și numitorul fracției la 10:

Am primit un răspuns frumos
Înmulțirea unei fracții cu un număr
Pentru a înmulți o fracție cu un număr, trebuie să înmulțiți numărătorul fracției cu acel număr și să lăsați numitorul același.
Exemplul 1. Înmulțiți o fracție cu numărul 1.
Înmulțiți numărătorul fracției cu numărul 1
![]()
Înregistrarea poate fi înțeleasă ca durând o jumătate de dată. De exemplu, dacă iei pizza o dată, primești pizza

Din legile înmulțirii știm că dacă multiplicandul și factorul sunt schimbate, produsul nu se va schimba. Dacă expresia este scrisă ca , atunci produsul va fi tot egal cu . Din nou, regula pentru înmulțirea unui număr întreg și a unei fracții funcționează:
![]()
Această notație poate fi înțeleasă ca luând jumătate din unu. De exemplu, dacă există 1 pizza întreagă și luăm jumătate din ea, atunci vom avea pizza:

Exemplul 2. Găsiți valoarea unei expresii
Înmulțiți numărătorul fracției cu 4
![]()
![]()
Expresia poate fi înțeleasă ca luând două sferturi de 4 ori. De exemplu, dacă iei 4 pizza, vei primi două pizza întregi

Și dacă schimbăm multiplicandul și multiplicatorul, obținem expresia . De asemenea, va fi egal cu 2. Această expresie poate fi înțeleasă ca luând două pizza din patru pizza întregi:

Înmulțirea fracțiilor
Pentru a înmulți fracțiile, trebuie să le înmulțiți numărătorii și numitorii. Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, trebuie să evidențiați întreaga parte a acestuia.
Exemplul 1. Găsiți valoarea expresiei.
![]()
Am primit un răspuns. Este recomandabil să reduceți această fracție. Fracția poate fi redusă cu 2. Apoi soluția finală va lua următoarea formă:

Expresia poate fi înțeleasă ca luând o pizza dintr-o jumătate de pizza. Să presupunem că avem jumătate de pizza:
Cum să iau două treimi din această jumătate? Mai întâi trebuie să împărțiți această jumătate în trei părți egale:

Și ia două din aceste trei bucăți:

Vom face pizza. Amintiți-vă cum arată pizza când este împărțită în trei părți:

O bucată din această pizza și cele două bucăți pe care le-am luat vor avea aceleași dimensiuni:

Cu alte cuvinte, vorbim de pizza de aceeași dimensiune. Prin urmare, valoarea expresiei este

Exemplul 2. Găsiți valoarea unei expresii
Înmulțiți numărătorul primei fracții cu numărătorul celei de-a doua fracții și numitorul primei fracții cu numitorul celei de-a doua fracții:

Răspunsul a fost o fracție improprie. Să evidențiem întreaga parte a acesteia:
![]()
Exemplul 3. Găsiți valoarea unei expresii
![]()
Răspunsul s-a dovedit a fi o fracție obișnuită, dar ar fi bine dacă ar fi scurtat. Pentru a reduce această fracție, ea trebuie împărțită la mcd-ul numărătorului și al numitorului. Deci, să găsim mcd-ul numerelor 105 și 450:
GCD pentru (105 și 150) este 15
Acum împărțim numărătorul și numitorul răspunsului nostru la mcd:
Reprezentarea unui număr întreg sub formă de fracție
Orice număr întreg poate fi reprezentat ca o fracție. De exemplu, numărul 5 poate fi reprezentat ca . Acest lucru nu va schimba sensul lui cinci, deoarece expresia înseamnă „numărul cinci împărțit la unu”, iar acesta, după cum știm, este egal cu cinci:
Numerele reciproce
Acum ne vom familiariza cu un subiect foarte interesant în matematică. Se numește „numere inverse”.
Definiţie. Invers la număr o este un număr care, atunci când este înmulțit cu o dă unul.
Să înlocuim în această definiție în locul variabilei o numărul 5 și încercați să citiți definiția:
Invers la număr 5 este un număr care, atunci când este înmulțit cu 5 dă unul.
Este posibil să găsim un număr care, înmulțit cu 5, dă unul? Se dovedește că este posibil. Să ne imaginăm cinci ca o fracție:
Apoi înmulțiți această fracție cu ea însăși, schimbați doar numărătorul și numitorul. Cu alte cuvinte, înmulțiți o fracție cu ea însăși, doar invers:
Ce se va întâmpla ca urmare a acestui fapt? Dacă continuăm să rezolvăm acest exemplu, obținem unul:
![]()
Aceasta înseamnă că inversul numărului 5 este numărul , deoarece atunci când înmulțiți 5 cu obțineți unul.
Reciproca unui număr poate fi găsită și pentru orice alt întreg.
- reciproca lui 3 este o fracție
- reciproca lui 4 este o fracție
Puteți găsi, de asemenea, reciproca oricărei alte fracții. Pentru a face acest lucru, doar întoarceți-l.
Înmulțirea unui număr întreg cu o fracție nu este o sarcină dificilă. Dar există subtilități pe care probabil le-ați înțeles la școală, dar de atunci le-ați uitat.
Cum se înmulțește un număr întreg cu o fracție - câțiva termeni
Dacă vă amintiți ce sunt numărătorul și numitorul și cum diferă o fracție proprie de o fracție improprie, săriți peste acest paragraf. Este pentru cei care au uitat complet teoria.
Numătorul este partea superioară a fracției - ceea ce împărțim. Numitorul este mai mic. Prin asta împărțim.
O fracție proprie este una al cărei numărător este mai mic decât numitorul ei. O fracție improprie este una al cărei numărător este mai mare sau egal cu numitorul său.
Cum se înmulțește un număr întreg cu o fracție
Regula pentru înmulțirea unui număr întreg cu o fracție este foarte simplă - înmulțim numărătorul cu numărul întreg, dar nu atingem numitorul. De exemplu: doi înmulțiți cu o cincime - obținem două cincimi. Patru înmulțit cu trei șaisprezecele este egal cu douăsprezece șaisprezece.


Reducere
În al doilea exemplu, fracția rezultată poate fi redusă.
Ce înseamnă? Vă rugăm să rețineți că atât numărătorul, cât și numitorul acestei fracții sunt divizibil cu patru. Împărțirea ambelor numere la un divizor comun se numește reducerea fracției. Primim trei sferturi.


Fracții improprii
Dar să presupunem că înmulțim patru cu două cincimi. S-a dovedit a fi opt cincimi. Aceasta este o fracție improprie.
Cu siguranță trebuie adus la forma corectă. Pentru a face acest lucru, trebuie să selectați o parte întreagă din ea.
Aici trebuie să utilizați diviziunea cu un rest. Primim unul și trei ca rest.
Un întreg și trei cincimi este fracția noastră potrivită.
Aducerea a treizeci și cinci de optimi la forma corectă este o sarcină puțin mai dificilă. Cel mai apropiat număr de treizeci și șapte care este divizibil cu opt este treizeci și doi. Când împărțim, obținem patru. Scădem treizeci și doi din treizeci și cinci și obținem trei. Rezultat: patru întregi și trei optime.


Egalitatea numărătorului și numitorului. Și aici totul este foarte simplu și frumos. Dacă numărătorul și numitorul sunt egali, rezultatul este pur și simplu unul.
Înmulțirea fracțiilor comune
Să ne uităm la un exemplu.
Să fie $\frac(1)(3)$ parte dintr-un măr pe o farfurie. Trebuie să găsim partea $\frac(1)(2)$ a acesteia. Partea necesară este rezultatul înmulțirii fracțiilor $\frac(1)(3)$ și $\frac(1)(2)$. Rezultatul înmulțirii a două fracții comune este o fracție comună.
Înmulțirea a două fracții ordinare
Regula pentru înmulțirea fracțiilor ordinare:
Rezultatul înmulțirii unei fracții cu o fracție este o fracție al cărei numărător este egal cu produsul numărătorilor fracțiilor înmulțite, iar numitorul este egal cu produsul numitorilor:
Exemplul 1
Efectuați înmulțirea fracțiilor comune $\frac(3)(7)$ și $\frac(5)(11)$.
Soluţie.
Să folosim regula pentru înmulțirea fracțiilor obișnuite:
\[\frac(3)(7)\cdot \frac(5)(11)=\frac(3\cdot 5)(7\cdot 11)=\frac(15)(77)\]
Răspuns:$\frac(15)(77)$
Dacă înmulțirea fracțiilor are ca rezultat o fracție reductibilă sau improprie, trebuie să o simplificați.
Exemplul 2
Înmulțiți fracțiile $\frac(3)(8)$ și $\frac(1)(9)$.
Soluţie.
Folosim regula pentru înmulțirea fracțiilor obișnuite:
\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)\]
Ca rezultat, am obținut o fracție reductibilă (pe baza împărțirii cu $3$. Împărțiți numărătorul și numitorul fracției la $3$, obținem:
\[\frac(3)(72)=\frac(3:3)(72:3)=\frac(1)(24)\]
Soluție scurtă:
\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)=\frac(1) (24)\]
Răspuns:$\frac(1)(24).$
Când înmulțiți fracții, puteți reduce numărătorii și numitorii până le găsiți produsul. În acest caz, numărătorul și numitorul fracției sunt descompuse în factori simpli, după care factorii care se repetă sunt anulați și se găsește rezultatul.
Exemplul 3
Calculați produsul fracțiilor $\frac(6)(75)$ și $\frac(15)(24)$.
Soluţie.
Să folosim formula pentru înmulțirea fracțiilor obișnuite:
\[\frac(6)(75)\cdot \frac(15)(24)=\frac(6\cdot 15)(75\cdot 24)\]
În mod evident, numărătorul și numitorul conțin numere care pot fi reduse în perechi la numerele $2$, $3$ și $5$. Să factorizăm numărătorul și numitorul în factori simpli și să facem o reducere:
\[\frac(6\cdot 15)(75\cdot 24)=\frac(2\cdot 3\cdot 3\cdot 5)(3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3)=\frac(1)(5\cdot 2\cdot 2)=\frac(1)(20)\]
Răspuns:$\frac(1)(20).$
Când înmulțiți fracții, puteți aplica legea comutativă:
Înmulțirea unei fracții comune cu un număr natural
Regula pentru înmulțirea unei fracții comune cu un număr natural:
Rezultatul înmulțirii unei fracții cu un număr natural este o fracție în care numărătorul este egal cu produsul numărătorului fracției înmulțite cu numărul natural, iar numitorul este egal cu numitorul fracției înmulțite:
unde $\frac(a)(b)$ este o fracție obișnuită, $n$ este un număr natural.
Exemplul 4
Înmulțiți fracția $\frac(3)(17)$ cu $4$.
Soluţie.
Să folosim regula pentru înmulțirea unei fracții obișnuite cu un număr natural:
\[\frac(3)(17)\cdot 4=\frac(3\cdot 4)(17)=\frac(12)(17)\]
Răspuns:$\frac(12)(17).$
Nu uitați să verificați rezultatul înmulțirii prin reductibilitatea fracției sau cu o fracție improprie.
Exemplul 5
Înmulțiți fracția $\frac(7)(15)$ cu numărul $3$.
Soluţie.
Să folosim formula pentru înmulțirea unei fracții cu un număr natural:
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)\]
Prin împărțirea la numărul $3$) putem determina că fracția rezultată poate fi redusă:
\[\frac(21)(15)=\frac(21:3)(15:3)=\frac(7)(5)\]
Drept urmare, am obținut o fracție necorespunzătoare. Să selectăm întreaga parte:
\[\frac(7)(5)=1\frac(2)(5)\]
Soluție scurtă:
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)=\frac(7)(5)=1\frac(2) (5)\]
Fracțiile pot fi reduse și prin înlocuirea numerelor din numărător și numitor cu descompunerea lor în factori primi. În acest caz, soluția ar putea fi scrisă după cum urmează:
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(7\cdot 3)(3\cdot 5)=\frac(7)(5)= 1\frac(2)(5)\]
Răspuns:$1\frac(2)(5).$
Când înmulți o fracție cu un număr natural, poți folosi legea comutativă:
Împărțirea fracțiilor
Operația de împărțire este inversul înmulțirii și rezultatul ei este o fracție prin care o fracție cunoscută trebuie înmulțită pentru a obține produsul cunoscut al două fracții.
Împărțirea a două fracții ordinare
Regula pentru împărțirea fracțiilor ordinare: Evident, numărătorul și numitorul fracției rezultate pot fi factorizate și reduse:
\[\frac(8\cdot 35)(15\cdot 12)=\frac(2\cdot 2\cdot 2\cdot 5\cdot 7)(3\cdot 5\cdot 2\cdot 2\cdot 3)= \frac(2\cdot 7)(3\cdot 3)=\frac(14)(9)\]
Ca rezultat, obținem o fracție necorespunzătoare, din care selectăm întreaga parte:
\[\frac(14)(9)=1\frac(5)(9)\]
Răspuns:$1\frac(5)(9).$