Lecția video „Exponent cu un exponent rațional” conține material educațional vizual pentru predarea unei lecții pe această temă. Lecția video conține informații despre conceptul de diplomă cu exponent rațional, proprietățile unor astfel de grade, precum și exemple care descriu utilizarea materialului educațional pentru a rezolva probleme practice. Scopul acestei lecții video este de a prezenta clar și clar materialul educațional, de a facilita dezvoltarea și memorarea acestuia de către elevi și de a dezvolta capacitatea de a rezolva probleme folosind conceptele învățate.

Principalele avantaje ale lecției video sunt capacitatea de a efectua vizual transformări și calcule, capacitatea de a folosi efecte de animație pentru a îmbunătăți eficiența învățării. Acompaniamentul vocal ajută la dezvoltarea unui discurs matematic corect și, de asemenea, face posibilă înlocuirea explicației profesorului, eliberându-l să efectueze munca individuală.

Lecția video începe prin introducerea subiectului. Când conectați studiul unui subiect nou cu material studiat anterior, se sugerează să ne amintim că n √a este altfel notat cu 1/n pentru n natural și a pozitiv. Această reprezentare n-rădăcină este afișată pe ecran. În continuare, se propune să luăm în considerare ce înseamnă expresia a m/n, în care a este un număr pozitiv, iar m/n este o fracție. Este dată definiția unui grad cu exponent rațional ca m/n = n √a m, evidențiată într-un cadru. Se observă că n poate fi un număr natural, iar m poate fi un număr întreg.

După definirea unui grad cu un exponent rațional, semnificația acestuia este dezvăluită prin exemple: (5/100) 3/7 = 7 √(5/100) 3. De asemenea, arată un exemplu în care o putere reprezentată printr-o zecimală este convertită într-o fracție pentru a fi reprezentată ca rădăcină: (1/7) 1,7 =(1/7) 17/10 = 10 √(1/7) 17 și un exemplu cu o putere negativă: 3 -1/8 = 8 √3 -1.

Particularitatea cazului special când baza gradului este zero este indicată separat. Se observă că acest grad are sens numai cu un exponent fracțional pozitiv. În acest caz, valoarea sa este zero: 0 m/n =0.

Se remarcă o altă caracteristică a unui grad cu un exponent rațional - că un grad cu un exponent fracționar nu poate fi considerat cu un exponent fracționar. Sunt date exemple de notare incorectă a gradelor: (-9) -3/7, (-3) -1/3, 0 -1/5.

În continuare, în lecția video discutăm proprietățile unui grad cu un exponent rațional. Se observă că proprietățile unui grad cu exponent întreg vor fi valabile și pentru un grad cu exponent rațional. Se propune reamintirea listei de proprietăți care sunt valabile și în acest caz:

1. La înmulțirea puterilor cu aceleași baze, exponenții lor se adună: a p a q =a p+q.
2. Împărțirea gradelor cu aceleași baze se reduce la un grad cu o bază dată și diferența de exponenți: a p:a q =a p-q.
3. Dacă ridicăm gradul la o anumită putere, atunci ajungem la un grad cu o bază dată și produsul exponenților: (a p) q =a pq.

Toate aceste proprietăți sunt valabile pentru puteri cu exponenți raționali p, q și bază pozitivă a>0. De asemenea, transformările de grade la deschiderea parantezelor rămân adevărate:

1. (ab) p =a p b p - ridicarea la o putere cu un exponent rațional a produsului a două numere se reduce la produsul numerelor, fiecare dintre acestea fiind ridicat la o putere dată.
2. (a/b) p =a p /b p - ridicarea unei fracții la o putere cu exponent rațional se reduce la o fracție al cărei numărător și numitor sunt ridicate la o putere dată.

Tutorialul video discută exemple de rezolvare care utilizează proprietățile considerate ale puterilor cu un exponent rațional. În primul exemplu, se propune găsirea valorii unei expresii care conține variabile x într-o putere fracționară: (x 1/6 -8) 2 -16x 1/6 (x -1/6 -1). În ciuda complexității expresiei, folosind proprietățile puterilor, aceasta poate fi rezolvată destul de simplu. Rezolvarea problemei începe cu simplificarea expresiei, care folosește regula ridicării unei puteri cu un exponent rațional la o putere, precum și înmulțirea puterilor cu aceeași bază. După înlocuirea valorii date x=8 în expresia simplificată x 1/3 +48, ​​este ușor să obțineți valoarea - 50.

În al doilea exemplu, trebuie să reduceți o fracție al cărei numărător și numitor conțin puteri cu un exponent rațional. Folosind proprietățile gradului, extragem din diferență factorul x 1/3, care apoi se reduce în numărător și numitor, iar folosind formula pentru diferența de pătrate, numărătorul este factorizat, ceea ce dă reduceri ulterioare de identice. factori la numărător și numitor. Rezultatul unor astfel de transformări este fracția scurtă x 1/4 +3.

Lecția video „Exponent cu un exponent rațional” poate fi folosită în loc ca profesorul să explice un nou subiect de lecție. Acest manual conține și informații suficient de complete pentru ca studentul să poată studia independent. Materialul poate fi util și pentru învățământul la distanță.

Expresii, conversie de expresii

Expresii de putere (expresii cu puteri) și transformarea lor

În acest articol vom vorbi despre conversia expresiilor cu puteri. În primul rând, ne vom concentra asupra transformărilor care sunt efectuate cu expresii de orice fel, inclusiv expresii de putere, cum ar fi deschiderea parantezelor și aducerea de termeni similari. Și apoi vom analiza transformările inerente în mod specific expresiilor cu grade: lucrul cu baza și exponentul, utilizarea proprietăților gradelor etc.

Navigare în pagină.

Ce sunt expresiile puterii?

Termenul „expresii de putere” practic nu apare în manualele școlare de matematică, dar apare destul de des în colecții de probleme, în special în cele destinate pregătirii pentru Examenul Unificat de Stat și Examenul Unificat de Stat, de exemplu. După analizarea sarcinilor în care este necesară efectuarea oricăror acțiuni cu expresii de putere, devine clar că expresiile de putere sunt înțelese ca expresii care conțin puteri în intrările lor. Prin urmare, puteți accepta următoarea definiție pentru dvs.:

Definiţie.

Expresii de putere sunt expresii care conțin puteri.

Să dăm exemple de expresii de putere. Mai mult, le vom prezenta în funcție de modul în care are loc dezvoltarea vederilor de la un grad cu exponent natural la un grad cu un exponent real.

După cum se știe, mai întâi se familiarizează cu puterea unui număr cu exponent natural în această etapă, primele expresii de putere cele mai simple de tip 3 2, 7 5 +1, (2+1) 5, (−0.1); 4, 3 a 2 apar −a+a 2 , x 3−1 , (a 2) 3 etc.

Puțin mai târziu, se studiază puterea unui număr cu exponent întreg, ceea ce duce la apariția expresiilor de putere cu puteri întregi negative, precum următoarele: 3 −2, , a −2 +2 b −3 +c 2 .

În liceu se întorc la grade. Acolo este introdus un grad cu exponent rațional, care presupune apariția expresiilor de putere corespunzătoare: , , etc. În sfârșit, se consideră grade cu exponenți iraționali și expresii care îi conțin: , .

Problema nu se limitează la expresiile de putere enumerate: mai departe variabila pătrunde în exponent și, de exemplu, apar următoarele expresii: 2 x 2 +1 sau . Și după ce ne-am familiarizat cu , încep să apară expresii cu puteri și logaritmi, de exemplu, x 2·lgx −5·x lgx.

Deci, ne-am ocupat de întrebarea ce reprezintă expresiile puterii. În continuare vom învăța să le transformăm.

Principalele tipuri de transformări ale expresiilor puterii

Cu expresii de putere, puteți efectua oricare dintre transformările de bază de identitate ale expresiilor. De exemplu, puteți deschide paranteze, puteți înlocui expresiile numerice cu valorile lor, puteți adăuga termeni similari etc. Desigur, în acest caz, este necesar să urmați procedura acceptată pentru efectuarea acțiunilor. Să dăm exemple.

Exemplu.

Calculați valoarea expresiei puterii 2 3 ·(4 2 −12) .

Soluţie.

În conformitate cu ordinea de execuție a acțiunilor, mai întâi efectuați acțiunile dintre paranteze. Acolo, în primul rând, înlocuim puterea 4 2 cu valoarea sa 16 (dacă este necesar, vezi), iar în al doilea rând, calculăm diferența 16−12=4. Avem 2 3 ·(4 2 −12)=2 3 ·(16−12)=2 3 ·4.

În expresia rezultată înlocuim puterea 2 3 cu valoarea ei 8, după care calculăm produsul 8·4=32. Aceasta este valoarea dorită.

Aşa, 2 3 ·(4 2 −12)=2 3 ·(16−12)=2 3 ·4=8·4=32.

Răspuns:

2 3 ·(4 2 −12)=32.

Exemplu.

Simplificați expresiile cu puteri 3 a 4 b −7 −1+2 a 4 b −7.

Soluţie.

Evident, această expresie conține termeni similari 3·a 4 ·b −7 și 2·a 4 ·b −7 , și îi putem prezenta: .

Răspuns:

3 a 4 b −7 −1+2 a 4 b −7 =5 a 4 b −7 −1.

Exemplu.

Exprimați o expresie cu puteri ca produs.

Soluţie.

Puteți face față sarcinii reprezentând numărul 9 ca o putere a lui 3 2 și apoi folosind formula de înmulțire abreviată - diferența de pătrate:

Răspuns:

Există, de asemenea, o serie de transformări identice inerente în mod specific expresiilor de putere. Le vom analiza mai departe.

Lucrul cu baza și exponent

Există puteri a căror bază și/sau exponent nu sunt doar numere sau variabile, ci unele expresii. Ca exemplu, dăm intrările (2+0.3·7) 5−3.7 și (a·(a+1)−a 2) 2·(x+1) .

Când lucrați cu astfel de expresii, puteți înlocui atât expresia din baza gradului, cât și expresia din exponent cu o expresie identică egală în ODZ a variabilelor sale. Cu alte cuvinte, după regulile cunoscute de noi, putem transforma separat baza gradului și separat exponentul. Este clar că în urma acestei transformări se va obține o expresie care este identic egală cu cea inițială.

Astfel de transformări ne permit să simplificăm expresiile cu puteri sau să atingem alte scopuri de care avem nevoie. De exemplu, în expresia de putere menționată mai sus (2+0.3 7) 5−3.7, puteți efectua operații cu numerele din bază și exponent, ceea ce vă va permite să treceți la puterea 4.1 1.3. Și după ce deschidem parantezele și aducem termeni similari la baza gradului (a·(a+1)−a 2) 2·(x+1) obținem o expresie a puterii de o formă mai simplă a 2·(x+1). ).

Utilizarea proprietăților gradului

Unul dintre instrumentele principale pentru transformarea expresiilor cu puteri sunt egalitățile care reflectă . Să le amintim pe cele principale. Pentru orice numere pozitive a și b și numere reale arbitrare r și s, următoarele proprietăți ale puterilor sunt adevărate:

• a r ·a s =a r+s ;
• a r:a s =a r−s ;
• (a·b) r =a r ·b r ;
• (a:b) r =a r:b r ;
• (a r) s =a r·s .

Rețineți că pentru exponenții naturali, întregi și pozitivi, restricțiile asupra numerelor a și b pot să nu fie atât de stricte. De exemplu, pentru numerele naturale m și n egalitatea a m ·a n =a m+n este adevărată nu numai pentru a pozitiv, ci și pentru negativ a și pentru a=0.

La școală, atunci când transformăm expresiile puterii, accentul principal este pe capacitatea de a alege proprietatea potrivită și de a o aplica corect. În acest caz, bazele gradelor sunt de obicei pozitive, ceea ce permite ca proprietățile gradelor să fie utilizate fără restricții. Același lucru este valabil și pentru transformarea expresiilor care conțin variabile în bazele puterilor - intervalul de valori admisibile ale variabilelor este de obicei astfel încât bazele să ia numai valori pozitive pe el, ceea ce vă permite să utilizați liber proprietățile puterilor . În general, trebuie să vă întrebați în mod constant dacă este posibil să utilizați vreo proprietate de grade în acest caz, deoarece utilizarea incorectă a proprietăților poate duce la o îngustare a valorii educaționale și la alte probleme. Aceste puncte sunt discutate în detaliu și cu exemple în articolul transformarea expresiilor folosind proprietățile grade. Aici ne vom limita la a lua în considerare câteva exemple simple.

Exemplu.

Exprimați expresia a 2,5 ·(a 2) −3:a −5,5 ca o putere cu baza a.

Soluţie.

Mai întâi, transformăm cel de-al doilea factor (a 2) −3 folosind proprietatea de a ridica o putere la o putere: (a 2) −3 =a 2·(−3) =a −6. Expresia originală a puterii va lua forma a 2,5 ·a −6:a −5,5. Evident, rămâne să folosim proprietățile înmulțirii și împărțirii puterilor cu aceeași bază, avem
a 2,5 ·a −6:a −5,5 =
a 2,5−6:a −5,5 =a −3,5:a −5,5 =
a −3,5−(−5,5) =a 2 .

Răspuns:

a 2,5 ·(a 2) −3:a −5,5 =a 2.

Proprietățile puterilor la transformarea expresiilor de putere sunt folosite atât de la stânga la dreapta, cât și de la dreapta la stânga.

Exemplu.

Găsiți valoarea expresiei puterii.

Soluţie.

Egalitatea (a·b) r =a r ·b r, aplicată de la dreapta la stânga, ne permite să trecem de la expresia originală la un produs al formei și mai departe. Și atunci când înmulțim puteri cu aceleași baze, exponenții se adună: .

A fost posibil să se transforme expresia originală într-un alt mod:

Răspuns:

.

Exemplu.

Având în vedere expresia puterii a 1.5 −a 0.5 −6 , introduceți o nouă variabilă t=a 0.5 .

Soluţie.

Puterea a 1,5 poate fi reprezentată ca 0,5·3 și apoi, pe baza proprietății unui grad la puterea (a r) s =a r·s, aplicată de la dreapta la stânga, se transformă în forma (a 0,5) 3 . Astfel, a 1,5 −a 0,5 −6=(a 0,5) 3 −a 0,5 −6. Acum este ușor să introduceți o nouă variabilă t=a 0,5, obținem t 3 −t−6.

Răspuns:

t 3 −t−6 .

Conversia fracțiilor care conțin puteri

Expresiile de putere pot conține sau reprezenta fracții cu puteri. Oricare dintre transformările de bază ale fracțiilor care sunt inerente fracțiilor de orice fel sunt pe deplin aplicabile acestor fracții. Adică, fracțiile care conțin puteri pot fi reduse, reduse la un nou numitor, lucrate separat cu numărătorul lor și separat cu numitorul etc. Pentru a ilustra aceste cuvinte, luați în considerare soluții pentru mai multe exemple.

Exemplu.

Simplificați exprimarea puterii .

Soluţie.

Această expresie a puterii este o fracție. Să lucrăm cu numărătorul și numitorul. La numărător deschidem parantezele și simplificăm expresia rezultată folosind proprietățile puterilor, iar la numitor prezentăm termeni similari:

Și să schimbăm și semnul numitorului punând un minus în fața fracției: .

Răspuns:

.

Reducerea fracțiilor care conțin puteri la un nou numitor se realizează în mod similar cu reducerea fracțiilor raționale la un nou numitor. În acest caz, se găsește și un factor suplimentar și se înmulțesc numărătorul și numitorul fracției cu acesta. Când efectuați această acțiune, merită să ne amintim că reducerea la un nou numitor poate duce la o îngustare a VA. Pentru a preveni acest lucru, este necesar ca factorul suplimentar să nu ajungă la zero pentru nicio valoare a variabilelor din variabilele ODZ pentru expresia originală.

Exemplu.

Reduceți fracțiile la un nou numitor: a) la numitorul a, b) la numitor.

Soluţie.

a) În acest caz, este destul de ușor să ne dăm seama care multiplicator suplimentar ajută la obținerea rezultatului dorit. Acesta este un multiplicator de 0,3, deoarece a 0,7 ·a 0,3 =a 0,7+0,3 =a. Rețineți că în intervalul de valori permise ale variabilei a (aceasta este mulțimea tuturor numerelor reale pozitive), puterea lui 0,3 nu dispare, prin urmare, avem dreptul de a înmulți numărătorul și numitorul unui anumit număr. fracție de acest factor suplimentar:

b) Aruncând o privire mai atentă la numitor, veți găsi că

iar înmulțirea acestei expresii cu va da suma cuburilor și , adică . Și acesta este noul numitor la care trebuie să reducem fracția inițială.

Așa am găsit un factor suplimentar. În intervalul de valori admisibile ale variabilelor x și y, expresia nu dispare, prin urmare, putem înmulți numărătorul și numitorul fracției cu aceasta:

Răspuns:

O) , b) .

De asemenea, nu este nimic nou în reducerea fracțiilor care conțin puteri: numărătorul și numitorul sunt reprezentați ca un număr de factori, iar aceiași factori ai numărătorului și numitorului sunt reduse.

Exemplu.

Reduceți fracția: a) , b).

Soluţie.

a) În primul rând, numărătorul și numitorul pot fi reduse cu numerele 30 și 45, care este egal cu 15. De asemenea, este evident posibil să se efectueze o reducere cu x 0,5 +1 și cu . Iată ce avem:

b) În acest caz, factori identici la numărător și numitor nu sunt imediat vizibili. Pentru a le obține, va trebui să efectuați transformări preliminare. În acest caz, ele constau în factorizarea numitorului folosind formula diferenței de pătrate:

Răspuns:

O)

b) .

Conversia fracțiilor la un nou numitor și reducerea fracțiilor sunt folosite în principal pentru a face lucruri cu fracții. Acțiunile sunt efectuate conform regulilor cunoscute. La adunarea (scăderea) fracțiilor, acestea se reduc la un numitor comun, după care se adună (se scad) numărătorii, dar numitorul rămâne același. Rezultatul este o fracție al cărei numărător este produsul numărătorilor, iar numitorul este produsul numitorilor. Împărțirea cu o fracție este înmulțirea cu inversul acesteia.

Exemplu.

Urmați pașii .

Soluţie.

În primul rând, scădem fracțiile din paranteze. Pentru a face acest lucru, îi aducem la un numitor comun, care este , după care scădem numărătorii:

Acum înmulțim fracțiile:

Evident, se poate reduce cu o putere de x 1/2, după care avem .

De asemenea, puteți simplifica expresia puterii în numitor folosind formula diferenței de pătrate: .

Răspuns:

Exemplu.

Simplificați expresia puterii .

Soluţie.

Evident, această fracție poate fi redusă cu (x 2,7 +1) 2, aceasta dă fracția . Este clar că trebuie făcut altceva cu puterile lui X. Pentru a face acest lucru, transformăm fracția rezultată într-un produs. Acest lucru ne oferă posibilitatea de a profita de proprietatea împărțirii puterilor cu aceleași baze: . Și la sfârșitul procesului, trecem de la ultimul produs la fracțiune.

Răspuns:

.

Și să mai adăugăm că este posibil, și în multe cazuri de dorit, să se transfere factori cu exponenți negativi de la numărător la numitor sau de la numitor la numărător, schimbând semnul exponentului. Astfel de transformări simplifică adesea acțiunile ulterioare. De exemplu, o expresie de putere poate fi înlocuită cu .

Conversia expresiilor cu rădăcini și puteri

Adesea, în expresiile în care sunt necesare unele transformări, sunt prezente și rădăcini cu exponenți fracționari alături de puteri. Pentru a transforma o astfel de expresie în forma dorită, în cele mai multe cazuri este suficient să mergem doar la rădăcini sau doar la puteri. Dar, din moment ce este mai convenabil să lucrezi cu puteri, acestea se mută de obicei de la rădăcini la puteri. Cu toate acestea, este recomandabil să efectuați o astfel de tranziție atunci când ODZ de variabile pentru expresia originală vă permite să înlocuiți rădăcinile cu puteri fără a fi nevoie să vă referiți la modul sau să împărțiți ODZ-ul în mai multe intervale (am discutat acest lucru în detaliu în trecerea articolului de la rădăcini la puteri și înapoi După ce ne-am familiarizat cu gradul cu exponent rațional se introduce un grad cu un exponent irațional, ceea ce ne permite să vorbim despre un grad cu un exponent real arbitrar În această etapă, începe să fie a studiat la scoala. functie exponentiala, care este dată analitic de o putere, a cărei bază este un număr, iar exponentul este o variabilă. Așadar, ne confruntăm cu expresii de putere care conțin numere în baza puterii, iar în exponent - expresii cu variabile și, firește, apare nevoia de a efectua transformări ale unor astfel de expresii.

Trebuie spus că transformarea expresiilor de tipul indicat trebuie de obicei efectuată la rezolvare ecuații exponențialeŞi inegalități exponențiale, iar aceste conversii sunt destul de simple. În majoritatea covârșitoare a cazurilor, acestea se bazează pe proprietățile gradului și vizează, în cea mai mare parte, introducerea unei noi variabile în viitor. Ecuația ne va permite să le demonstrăm 5 2 x+1 −3 5 x 7 x −14 7 2 x−1 =0.

În primul rând, puterile, în exponenții cărora este suma unei anumite variabile (sau expresii cu variabile) și a unui număr, sunt înlocuite cu produse. Acest lucru se aplică primului și ultimului termeni ai expresiei din partea stângă:
5 2 x 5 1 −3 5 x 7 x −14 7 2 x 7 −1 =0,
5 5 2 x −3 5 x 7 x −2 7 2 x =0.

În continuare, ambele părți ale egalității sunt împărțite la expresia 7 2 x, care pe ODZ a variabilei x pentru ecuația originală ia doar valori pozitive (aceasta este o tehnică standard pentru rezolvarea ecuațiilor de acest tip, nu suntem vorbind despre asta acum, așa că concentrează-te pe transformările ulterioare ale expresiilor cu puteri ):

Acum putem anula fracții cu puteri, ceea ce dă .

În cele din urmă, raportul puterilor cu aceiași exponenți este înlocuit cu puteri de relații, rezultând ecuația , care este echivalent . Transformările efectuate ne permit să introducem o nouă variabilă, care reduce soluția ecuației exponențiale inițiale la soluția unei ecuații pătratice

I. V. Boykov, L. D. Romanova Culegere de sarcini pentru pregătirea pentru examenul de stat unificat. Partea 1. Penza 2003.

Expresia a n (putere cu un exponent întreg) va fi definită în toate cazurile, cu excepția cazului în care a = 0 și n este mai mic sau egal cu zero.

Proprietățile grade

Proprietățile de bază ale grade cu un exponent întreg:

a m *a n = a (m+n);

a m: a n = a (m-n) (cu o nu este egal cu zero);

(a m) n = a (m*n) ;

(a*b) n = a n *b n ;

(a/b) n = (a n)/(b n) (cu b nu este egal cu zero);

a 0 = 1 (cu o nu este egal cu zero);

Aceste proprietăți vor fi valabile pentru orice numere a, b și orice numere întregi m și n. De asemenea, este de remarcat următoarea proprietate:

Dacă m>n, atunci a m > a n, pentru a>1 și a m

Putem generaliza conceptul de putere a unui număr în cazurile în care numerele raționale acționează ca exponent. În același timp, aș dori ca toate proprietățile de mai sus să fie îndeplinite, sau măcar unele dintre ele.

De exemplu, dacă ar fi îndeplinită proprietatea (a m) n = a (m*n), următoarea egalitate ar fi valabilă:

(a (m/n)) n = a m .

Această egalitate înseamnă că numărul a (m/n) trebuie să fie rădăcina a n-a a numărului a m.

Puterea unui număr a (mai mare decât zero) cu un exponent rațional r = (m/n), unde m este un număr întreg, n este un număr natural mai mare decât unu, este numărul n√(a m). Pe baza definiției: a (m/n) = n√(a m).

Pentru toate r pozitive, se va determina puterea lui zero. Prin definiție, 0 r = 0. Rețineți, de asemenea, că pentru orice număr întreg, orice m și n natural și pozitiv O următoarea egalitate este adevărată: a (m/n) = a ((mk)/(nk)) .

De exemplu: 134 (3/4) = 134 (6/8) = 134 (9/12).

Din definiția unui grad cu exponent rațional rezultă direct că pentru orice a pozitiv și orice r rațional numărul a r va fi pozitiv.

Proprietățile de bază ale unui grad cu exponent rațional

Pentru orice numere raționale p, q și orice a>0 și b>0 sunt adevărate următoarele egalități:

1. (a p)*(a q) = a (p+q) ;

2. (a p):(b q) = a (p-q) ;

3. (a p) q = a (p*q) ;

4. (a*b) p = (a p)*(b p);

5. (a/b) p = (a p)/(b p).

Aceste proprietăți decurg din proprietățile rădăcinilor. Toate aceste proprietăți sunt dovedite într-un mod similar, așa că ne vom limita la a demonstra doar una dintre ele, de exemplu, prima (a p)*(a q) = a (p + q) .

Fie p = m/n și q = k/l, unde n, l sunt numere naturale și m, k sunt numere întregi. Atunci trebuie să dovediți că:

(a (m/n))*(a (k/l)) = a ((m/n) + (k/l)) .

Mai întâi, să aducem fracțiile m/n k/l la un numitor comun. Obținem fracțiile (m*l)/(n*l) și (k*n)/(n*l). Să rescriem partea stângă a egalității folosind aceste notații și obținem:

(a (m/n))*(a (k/l)) = (a ((m*l)/(n*l)))*(a ((k*n)/(n*l)) ).

(a (m/n))*(a (k/l)) = (a ((m*l)/(n*l)))*(a ((k*n)/(n*l)) ) = (n*l)√(a (m*l))*(n*l)√(a (k*n)) = (n*l)√((a (m*l))*(a (k*n))) = (n*l)√(a (m*l+k*n)) = a ((m*l+k*n)/(n*l)) = a ((m /n)+(k/l)).

Lecția nr. 30 (Algebră și analiză de bază, clasa a XI-a)

Subiectul lecției: Grad cu un exponent rațional.

Obiectivul lecției: 1 . Extindeți conceptul de grad, dați conceptul de grad cu un exponent rațional; învață cum să transformi un grad cu un exponent rațional într-o rădăcină și invers; calcula puteri cu exponent rațional.

2. Dezvoltarea memoriei și a gândirii.

3. Formarea activității.

„Lasă pe cineva să încerce să tache

de la matematică și va vedea,

Că nu vei ajunge departe fără ele” M.V. Lomonosov

Progresul lecției.

I. Enunțarea temei și a scopului lecției.

II. Repetarea și consolidarea materialului acoperit.

1. Analiza exemplelor de acasă nerezolvate.

2. Supravegherea muncii independente:

Opțiunea 1.

1. Rezolvați ecuația: √(2x – 1) = 3x – 12

2. Rezolvați inegalitatea: √(3x – 2) ≥ 4 – x

Opțiunea 2.

1. Rezolvați ecuația: 3 – 2x = √(7x + 32)

2. Rezolvați inegalitatea: √(3x + 1) ≥ x – 1

III. Învățarea de materiale noi.

1 . Să ne amintim extinderea conceptului de numere: N є Z є Q є R.

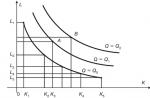
Acest lucru este cel mai bine reprezentat de diagrama de mai jos:

Natural (N)

Zero

Numerele nenegative

Numerele negative

Numerele fracționale

numere întregi (Z)

Iraţional

Rațional (Q)

Numerele reale

2. În clasele inferioare a fost definit conceptul de putere a unui număr cu exponent întreg. a) Amintiți-vă definiția exponentului a) cu un natural, b) cu un întreg negativ, c) cu un exponent zero.Subliniați că expresia a n are sens pentru toate numerele întregi n și orice valori ale lui a, cu excepția a=0 și n≤0.

b) Enumerați proprietățile gradelor cu exponent întreg.

3. Lucru oral.

1). Calculați: 1 -5 ; 4 -3; (-10) 0; (-5) -2; (1/2) -4; (3/7) -1 .

2). Scrie-o ca o putere cu exponent negativ:

1/4 5 ;1/21 3 ; 1/x 7; 1/a 9 .

3). Comparați cu unitatea: 12-3 ; 21 0 ; (0,6) -5 ; (5/19) -4 .

4 . Acum trebuie să înțelegeți sensul expresiilor 3 0,4 ; 4 5/7 ; 5 -1/2 etc. Pentru a face acest lucru, este necesar să se generalizeze conceptul de grad în așa fel încât toate proprietățile enumerate ale grade să fie satisfăcute. Luați în considerare egalitatea (a m/n ) n = a m . Apoi, prin definiția rădăcinii a n-a, este rezonabil să presupunem că a m/n va fi a n-a rădăcină a lui a m . Este dată o definiție a gradului cu un exponent rațional.

5. Luați în considerare exemplele 1 și 2 din manual.

6. Să facem o serie de comentarii legate de conceptul de grad cu exponent rațional.

Nota 1 : Pentru orice a>0 și număr rațional r, numărul a r >0

Nota 2 : Prin proprietatea de bază a fracțiilor, numărul rațional m/n poate fi scris ca mk/nk pentru orice număr natural k. Apoivaloarea gradului nu depinde de forma de scriere a numărului rațional, deoarece a mk/nk = = nk √a mk = n √a m = a m/n

Nota 3: Când a Să explicăm acest lucru cu un exemplu. Luați în considerare (-64) 1/3 = 3 √-64 = -4. Pe de altă parte: 1/3 = 2/6 și apoi (-64) 1/ 3 = (-64) 2/6 = 6 √(-64) 2 = 6√64 2 = 6 √4 6 = 4. Obținem o contradicție.