Exemple de inegalități logaritmice. Inegalități logaritmice complexe

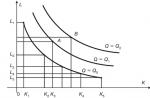
Adesea, la rezolvarea inegalităților logaritmice, există probleme cu o bază logaritmică variabilă. Astfel, o inegalitate a formei

este o inegalitate școlară standard. De regulă, pentru a o rezolva, se utilizează o tranziție la un set echivalent de sisteme:

Dezavantajul acestei metode este necesitatea de a rezolva șapte inegalități, fără a număra două sisteme și o populație. Deja cu aceste funcții pătratice, rezolvarea populației poate dura mult timp.

Este posibil să se propună o modalitate alternativă, mai puțin consumatoare de timp pentru a rezolva această inegalitate standard. Pentru a face acest lucru, luăm în considerare următoarea teoremă.

Teorema 1. Să existe o funcție crescătoare continuă pe o mulțime X. Atunci pe această mulțime semnul incrementului funcției va coincide cu semnul incrementului argumentului, adică. , Unde .

Notă: dacă o funcție descrescătoare continuă pe un set X, atunci .

Să revenim la inegalitate. Să trecem la logaritmul zecimal (puteți trece la oricare cu o bază constantă mai mare de unu).

Acum puteți folosi teorema, observând creșterea funcțiilor în numărător iar în numitor. Deci este adevărat

Ca urmare, numărul de calcule care duc la răspuns este redus cu aproximativ jumătate, ceea ce economisește nu numai timp, ci și vă permite să faceți mai puține erori aritmetice și neglijente.

Exemplul 1.

Comparând cu (1) găsim , , .

Trecând la (2) vom avea:

Exemplul 2.

Comparând cu (1) găsim , , .

Trecând la (2) vom avea:

Exemplul 3.

Deoarece partea stângă a inegalității este o funcție crescătoare ca și , atunci răspunsul va fi multe.

Numeroasele exemple în care Tema 1 poate fi aplicată pot fi extinse cu ușurință ținând cont de Tema 2.

Lasă pe platou X se definesc functiile , , , iar pe acest set semnele si coincid, i.e. , atunci va fi corect.

Exemplul 4.

Exemplul 5.

Cu abordarea standard, exemplul este rezolvat după următoarea schemă: produsul este mai mic decât zero atunci când factorii sunt de semne diferite. Aceste. se consideră un set de două sisteme de inegalități, în care, așa cum sa indicat la început, fiecare inegalitate se descompune în încă șapte.

Dacă luăm în considerare teorema 2, atunci fiecare dintre factori, ținând cont de (2), poate fi înlocuit cu o altă funcție care are același semn în acest exemplu O.D.Z.

Metoda de înlocuire a incrementului unei funcții cu un increment de argument, ținând cont de Teorema 2, se dovedește a fi foarte convenabilă atunci când se rezolvă probleme tipice C3 Unified State Examination.

Exemplul 6.

Exemplul 7.

. Să notăm. Primim

. Rețineți că înlocuirea implică: . Revenind la ecuație, obținem .

Exemplul 8.

În teoremele pe care le folosim nu există restricții privind clasele de funcții. În acest articol, ca exemplu, teoremele au fost aplicate pentru rezolvarea inegalităților logaritmice. Următoarele câteva exemple vor demonstra promisiunea metodei de rezolvare a altor tipuri de inegalități.

Crezi că mai este timp până la Examenul Unificat de Stat și vei avea timp să te pregătești? Poate că așa este. Dar, în orice caz, cu cât studentul începe mai devreme pregătirea, cu atât trece cu mai mult succes examenele. Astăzi am decis să dedicăm un articol inegalităților logaritmice. Aceasta este una dintre sarcini, ceea ce înseamnă o oportunitate de a obține credit suplimentar.

Știți deja ce este un logaritm? Chiar sperăm că da. Dar chiar dacă nu ai un răspuns la această întrebare, nu este o problemă. Înțelegerea a ceea ce este un logaritm este foarte simplă.

De ce 4? Trebuie să ridicați numărul 3 la această putere pentru a obține 81. Odată ce înțelegeți principiul, puteți trece la calcule mai complexe.

Ai trecut prin inegalități în urmă cu câțiva ani. Și de atunci le-ai întâlnit constant la matematică. Dacă aveți probleme în rezolvarea inegalităților, consultați secțiunea corespunzătoare.
Acum că ne-am familiarizat cu conceptele în mod individual, să trecem la analizarea lor în general.

Cea mai simplă inegalitate logaritmică.

Cele mai simple inegalități logaritmice nu se limitează la acest exemplu, există încă trei, doar cu semne diferite. De ce este necesar acest lucru? Pentru a înțelege mai bine cum se rezolvă inegalitățile cu logaritmi. Acum să dăm un exemplu mai aplicabil, încă destul de simplu, vom lăsa inegalitățile logaritmice complexe pentru mai târziu.

Cum să rezolvi asta? Totul începe cu ODZ. Merită să știți mai multe despre asta dacă doriți să rezolvați întotdeauna cu ușurință orice inegalitate.

Ce este ODZ? ODZ pentru inegalitățile logaritmice

Abrevierea reprezintă intervalul de valori acceptabile. Această formulare apare adesea în sarcinile pentru examenul de stat unificat. ODZ vă va fi de folos nu numai în cazul inegalităților logaritmice.

Privește din nou exemplul de mai sus. Vom lua în considerare ODZ pe baza acestuia, astfel încât să înțelegeți principiul, iar rezolvarea inegalităților logaritmice nu ridică întrebări. Din definiția unui logaritm rezultă că 2x+4 trebuie să fie mai mare decât zero. În cazul nostru, aceasta înseamnă următoarele.

Acest număr, prin definiție, trebuie să fie pozitiv. Rezolvați inegalitatea prezentată mai sus. Acest lucru se poate face chiar și oral, aici este clar că X nu poate fi mai mic de 2. Soluția inegalității va fi definirea intervalului de valori acceptabile.
Acum să trecem la rezolvarea celei mai simple inegalități logaritmice.

Aruncăm logaritmii înșiși din ambele părți ale inegalității. Cu ce ​​ne lasă asta? Inegalitate simplă.

Nu este greu de rezolvat. X trebuie să fie mai mare de -0,5. Acum combinăm cele două valori obținute într-un sistem. Astfel,

Acesta va fi intervalul de valori acceptabile pentru inegalitatea logaritmică luată în considerare.

De ce avem nevoie de ODZ? Aceasta este o oportunitate de a elimina răspunsurile incorecte și imposibile. Dacă răspunsul nu se află în intervalul de valori acceptabile, atunci răspunsul pur și simplu nu are sens. Acest lucru merită amintit mult timp, deoarece în examenul de stat unificat este adesea nevoie de căutarea ODZ și nu se referă numai la inegalitățile logaritmice.

Algoritm pentru rezolvarea inegalității logaritmice

Soluția constă din mai multe etape. În primul rând, trebuie să găsiți intervalul de valori acceptabile. Vor fi două semnificații în ODZ, despre care am discutat mai sus. În continuare trebuie să rezolvăm inegalitatea în sine. Metodele de rezolvare sunt următoarele:

• metoda de înlocuire a multiplicatorului;
• descompunere;
• metoda de raționalizare.

În funcție de situație, merită să utilizați una dintre metodele de mai sus. Să trecem direct la soluție. Să dezvăluim cea mai populară metodă, care este potrivită pentru rezolvarea sarcinilor de examinare unificată de stat în aproape toate cazurile. În continuare ne vom uita la metoda de descompunere. Vă poate ajuta dacă întâlniți o inegalitate deosebit de complicată. Deci, un algoritm pentru rezolvarea inegalității logaritmice.

Exemple de soluții :

Nu degeaba am luat exact această inegalitate! Atenție la bază. Amintiți-vă: dacă este mai mare decât unu, semnul rămâne același la găsirea intervalului de valori acceptabile; în caz contrar, trebuie să schimbați semnul inegalității.

Ca rezultat, obținem inegalitatea:

Acum reducem partea stângă la forma ecuației egală cu zero. În loc de semnul „mai puțin decât” punem „egal” și rezolvăm ecuația. Astfel, vom găsi ODZ. Sperăm că nu veți avea probleme la rezolvarea unei astfel de ecuații simple. Răspunsurile sunt -4 și -2. Asta nu e tot. Trebuie să afișați aceste puncte pe grafic, plasând „+” și „-”. Ce trebuie făcut pentru asta? Înlocuiți numerele din intervale în expresie. Acolo unde valorile sunt pozitive, punem „+” acolo.

Răspuns: x nu poate fi mai mare de -4 și mai mic de -2.

Am găsit intervalul de valori acceptabile doar pentru partea stângă, acum trebuie să găsim intervalul de valori acceptabile pentru partea dreaptă. Acest lucru este mult mai ușor. Raspuns: -2. Intersectăm ambele zone rezultate.

Și abia acum începem să abordăm inegalitatea în sine.

Să simplificăm cât mai mult posibil pentru a fi mai ușor de rezolvat.

Folosim din nou metoda intervalului în soluție. Să sărim peste calcule; totul este deja clar din exemplul anterior. Răspuns.

Dar această metodă este potrivită dacă inegalitatea logaritmică are aceleași baze.

Rezolvarea ecuațiilor logaritmice și a inegalităților cu baze diferite necesită o reducere inițială la aceeași bază. Apoi, utilizați metoda descrisă mai sus. Dar există un caz mai complicat. Să luăm în considerare unul dintre cele mai complexe tipuri de inegalități logaritmice.

Inegalități logaritmice cu bază variabilă

Cum se rezolvă inegalitățile cu astfel de caracteristici? Da, și astfel de persoane pot fi găsite în examenul de stat unificat. Rezolvarea inegalităților în felul următor va avea, de asemenea, un efect benefic asupra procesului tău educațional. Să ne uităm la problema în detaliu. Să renunțăm la teoria și să trecem direct la practică. Pentru a rezolva inegalitățile logaritmice, este suficient să vă familiarizați o dată cu exemplul.

Pentru a rezolva o inegalitate logaritmică a formei prezentate, este necesar să se reducă partea dreaptă la un logaritm cu aceeași bază. Principiul seamănă cu tranzițiile echivalente. Ca urmare, inegalitatea va arăta astfel.

De fapt, tot ce rămâne este să creăm un sistem de inegalități fără logaritmi. Folosind metoda raționalizării, trecem la un sistem echivalent de inegalități. Veți înțelege regula în sine atunci când înlocuiți valorile corespunzătoare și urmăriți modificările acestora. Sistemul va avea următoarele inegalități.

Când utilizați metoda raționalizării la rezolvarea inegalităților, trebuie să vă amintiți următoarele: unul trebuie să fie scăzut din bază, x, prin definiția logaritmului, este scăzut din ambele părți ale inegalității (dreapta de la stânga), două expresii sunt înmulțite și pus sub semnul original în raport cu zero.

Soluția ulterioară se realizează folosind metoda intervalului, totul este simplu aici. Este important să înțelegeți diferențele dintre metodele de soluție, apoi totul va începe să funcționeze ușor.

Există multe nuanțe în inegalitățile logaritmice. Cele mai simple dintre ele sunt destul de ușor de rezolvat. Cum le poți rezolva pe fiecare fără probleme? Ați primit deja toate răspunsurile din acest articol. Acum ai un antrenament lung în față. Exersați în mod constant rezolvarea unei varietăți de probleme în cadrul examenului și veți putea obține cel mai mare scor. Mult succes în sarcina ta grea!

Dintre întreaga varietate de inegalități logaritmice, inegalitățile cu bază variabilă sunt studiate separat. Ele sunt rezolvate folosind o formulă specială, care din anumite motive este rareori predată la școală:

log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0

În loc de caseta de selectare „∨”, puteți pune orice semn de inegalitate: mai mult sau mai puțin. Principalul lucru este că în ambele inegalități semnele sunt aceleași.

Astfel scăpăm de logaritmi și reducem problema la o inegalitate rațională. Acesta din urmă este mult mai ușor de rezolvat, dar atunci când se aruncă logaritmi, pot apărea rădăcini suplimentare. Pentru a le tăia, este suficient să găsiți intervalul de valori acceptabile. Dacă ați uitat ODZ al unui logaritm, vă recomand cu tărie să îl repetați - vedeți „Ce este un logaritm”.

Tot ceea ce are legătură cu intervalul de valori acceptabile trebuie scris și rezolvat separat:

f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.

Aceste patru inegalități constituie un sistem și trebuie satisfăcute simultan. Când a fost găsit intervalul de valori acceptabile, tot ce rămâne este să îl intersectăm cu soluția inegalității raționale - și răspunsul este gata.

Sarcină. Rezolvați inegalitatea:

Mai întâi, să scriem ODZ al logaritmului:

Primele două inegalități sunt satisfăcute automat, dar ultima va trebui scrisă. Deoarece pătratul unui număr este zero dacă și numai dacă numărul însuși este zero, avem:

x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.

Rezultă că ODZ a logaritmului este toate numerele cu excepția zero: x ∈ (−∞ 0)∪(0; +∞). Acum rezolvăm inegalitatea principală:

Facem tranziția de la inegalitatea logaritmică la una rațională. Inegalitatea originală are un semn „mai puțin decât”, ceea ce înseamnă că inegalitatea rezultată trebuie să aibă și un semn „mai puțin decât”. Avem:

(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x ) (3 + x ) x 2< 0.

Zerourile acestei expresii sunt: ​​x = 3; x = −3; x = 0. Mai mult, x = 0 este o rădăcină a celei de-a doua multiplicități, ceea ce înseamnă că la trecerea prin aceasta, semnul funcției nu se schimbă. Avem:

Se obține x ∈ (−∞ −3)∪(3; +∞). Acest set este complet conținut în ODZ al logaritmului, ceea ce înseamnă că acesta este răspunsul.

Conversia inegalităților logaritmice

Adesea inegalitatea originală este diferită de cea de mai sus. Acest lucru poate fi corectat cu ușurință folosind regulile standard pentru lucrul cu logaritmi - vezi „Proprietățile de bază ale logaritmilor”. Anume:

1. Orice număr poate fi reprezentat ca un logaritm cu o bază dată;
2. Suma și diferența logaritmilor cu aceleași baze pot fi înlocuite cu un logaritm.

Separat, aș dori să vă reamintesc intervalul de valori acceptabile. Deoarece pot exista mai mulți logaritmi în inegalitatea inițială, este necesar să se găsească VA a fiecăruia dintre ei. Astfel, schema generală de rezolvare a inegalităților logaritmice este următoarea:

1. Aflați VA fiecărui logaritm inclus în inegalitate;
2. Reduceți inegalitatea la una standard folosind formulele de adunare și scădere a logaritmilor;
3. Rezolvați inegalitatea rezultată folosind schema dată mai sus.

Sarcină. Rezolvați inegalitatea:

Să găsim domeniul de definiție (DO) al primului logaritm:

Rezolvăm folosind metoda intervalului. Aflarea zerourilor numărătorului:

3x − 2 = 0;
x = 2/3.

Apoi - zerourile numitorului:

x − 1 = 0;
x = 1.

Marcam zerouri și semne pe săgeata de coordonate:

Se obține x ∈ (−∞ 2/3)∪(1; +∞). Al doilea logaritm va avea același VA. Dacă nu crezi, poți să verifici. Acum transformăm al doilea logaritm astfel încât baza să fie două:

După cum puteți vedea, cei trei de la bază și în fața logaritmului au fost reduse. Avem doi logaritmi cu aceeași bază. Să le adunăm:

log 2 (x − 1) 2< 2;
log 2 (x − 1) 2< log 2 2 2 .

Am obținut inegalitatea logaritmică standard. Scăpăm de logaritmi folosind formula. Deoarece inegalitatea originală conține un semn „mai puțin decât”, expresia rațională rezultată trebuie, de asemenea, să fie mai mică decât zero. Avem:

(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2)(2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).

Avem două seturi:

1. ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
2. Răspunsul candidatului: x ∈ (−1; 3).

Rămâne să intersectăm aceste mulțimi - obținem răspunsul real:

Suntem interesați de intersecția mulțimilor, așa că selectăm intervale care sunt umbrite pe ambele săgeți. Se obține x ∈ (−1; 2/3)∪(1; 3) - toate punctele sunt perforate.

Menținerea confidențialității dvs. este importantă pentru noi. Din acest motiv, am dezvoltat o Politică de confidențialitate care descrie modul în care folosim și stocăm informațiile dumneavoastră. Vă rugăm să examinați practicile noastre de confidențialitate și să ne comunicați dacă aveți întrebări.

Colectarea și utilizarea informațiilor personale

Informațiile personale se referă la date care pot fi folosite pentru a identifica sau contacta o anumită persoană.

Vi se poate cere să furnizați informațiile dumneavoastră personale în orice moment când ne contactați.

Mai jos sunt câteva exemple de tipuri de informații personale pe care le putem colecta și cum putem folosi aceste informații.

Ce informații personale colectăm:

• Când trimiteți o cerere pe site, este posibil să colectăm diverse informații, inclusiv numele dvs., numărul de telefon, adresa de e-mail etc.

Cum folosim informațiile dumneavoastră personale:

• Informațiile personale pe care le colectăm ne permit să vă contactăm cu oferte unice, promoții și alte evenimente și evenimente viitoare.
• Din când în când, putem folosi informațiile dumneavoastră personale pentru a trimite notificări și comunicări importante.
• De asemenea, putem folosi informații personale în scopuri interne, cum ar fi efectuarea de audituri, analize de date și diverse cercetări pentru a îmbunătăți serviciile pe care le oferim și pentru a vă oferi recomandări cu privire la serviciile noastre.
• Dacă participați la o tragere la sorți, la un concurs sau la o promoție similară, este posibil să folosim informațiile pe care le furnizați pentru a administra astfel de programe.

Dezvăluirea informațiilor către terți

Nu dezvăluim informațiile primite de la dumneavoastră către terți.

Excepții:

• Dacă este necesar - în conformitate cu legea, procedura judiciară, în cadrul procedurilor judiciare și/sau pe baza solicitărilor publice sau a solicitărilor din partea autorităților guvernamentale de pe teritoriul Federației Ruse - să vă dezvăluiți informațiile personale. De asemenea, putem dezvălui informații despre dumneavoastră dacă stabilim că o astfel de dezvăluire este necesară sau adecvată pentru securitate, aplicarea legii sau alte scopuri de importanță publică.
• În cazul unei reorganizări, fuziuni sau vânzări, este posibil să transferăm informațiile personale pe care le colectăm terței părți succesoare aplicabile.

Protecția informațiilor personale

Luăm măsuri de precauție - inclusiv administrative, tehnice și fizice - pentru a vă proteja informațiile personale împotriva pierderii, furtului și utilizării greșite, precum și împotriva accesului, dezvăluirii, modificării și distrugerii neautorizate.

Respectarea vieții private la nivelul companiei

Pentru a ne asigura că informațiile dumneavoastră personale sunt în siguranță, comunicăm angajaților noștri standarde de confidențialitate și securitate și aplicăm strict practicile de confidențialitate.

O inegalitate se numește logaritmică dacă conține o funcție logaritmică.

Metodele de rezolvare a inegalităților logaritmice nu sunt diferite de, cu excepția a două lucruri.

În primul rând, când se trece de la inegalitatea logaritmică la inegalitatea funcțiilor sublogaritmice, ar trebui urmați semnul inegalității rezultate. Se supune următoarei reguli.

Dacă baza funcției logaritmice este mai mare de $1$, atunci când treceți de la inegalitatea logaritmică la inegalitatea funcțiilor sublogaritmice, semnul inegalității se păstrează, dar dacă este mai mic de $1$, atunci se schimbă la opus .

În al doilea rând, soluția oricărei inegalități este un interval și, prin urmare, la sfârșitul rezolvării inegalității funcțiilor sublogaritmice este necesar să se creeze un sistem de două inegalități: prima inegalitate a acestui sistem va fi inegalitatea funcțiilor sublogaritmice, iar al doilea va fi intervalul domeniului de definire a funcţiilor logaritmice incluse în inegalitatea logaritmică.

Practica.

Să rezolvăm inegalitățile:

1. $\log_(2)((x+3)) \geq 3.$

$D(y): \x+3>0.$

$x \in (-3;+\infty)$

Baza logaritmului este $2>1$, deci semnul nu se schimbă. Folosind definiția logaritmului, obținem:

$x+3 \geq 2^(3),$

$x \in )